|
| |
Приведенное далее
описание базируется на материалах из книги
NUMERICAL RECEPIES
Метод
вычисления интегралов с быстро осциллирующей функцией
(Фурье-подобных интегралов)
Очень часто возникает необходимость
вычислить точное числовое значение интеграла вида
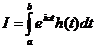 (П1.1)
(П1.1)
и необходимо проводить это вычисление для
большого числа значений 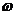 .
Во многих практических случаях функция .
Во многих практических случаях функция
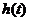 является
гладкой на интервале является
гладкой на интервале 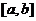 ,
но она не является периодической на этом интервале и не равна нулю на обоих
концах его. Поэтому использование быстрого преобразования Фурье для вычисления
таких интегралов, как будет показано далее, является заманчивой, но не
тривиальной задачей. ,
но она не является периодической на этом интервале и не равна нулю на обоих
концах его. Поэтому использование быстрого преобразования Фурье для вычисления
таких интегралов, как будет показано далее, является заманчивой, но не
тривиальной задачей.
Рассмотрим сначала простейший подход к проблеме,
чтобы понять, где возникают трудности. Разобьем интервал
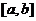 на на
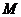 подинтервалов,
где подинтервалов,
где 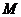 –
большое целое число, и определим величины –
большое целое число, и определим величины
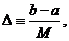
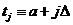 , ,
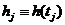 , ,
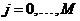 (П1.2)
(П1.2)
Отметим, что
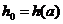 , ,
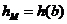 и
имеется и
имеется 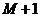 значение значение
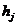 .
Мы можем аппроксимировать интеграл (П1.1) суммой .
Мы можем аппроксимировать интеграл (П1.1) суммой
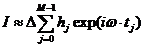 ,
(П1.3) ,
(П1.3)
причем это в любом случае аппроксимация 1-го
порядка. (Если мы центрируем значения
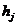 и и
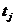 ,
мы получим аппроксимацию второго порядка). Для определенных значений ,
мы получим аппроксимацию второго порядка). Для определенных значений
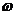 и и
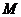 уравнение
(П.1.3) может быть превращено в выражение для дискретного преобразования Фурье,
или ДПФ, и его вычисление можно выполнить с помощью алгоритма быстрого
преобразования Фурье (БПФ). В частности мы можем выбрать уравнение
(П.1.3) может быть превращено в выражение для дискретного преобразования Фурье,
или ДПФ, и его вычисление можно выполнить с помощью алгоритма быстрого
преобразования Фурье (БПФ). В частности мы можем выбрать
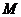 такое,
чтобы оно было целой степенью 2, и определить специальную последовательность такое,
чтобы оно было целой степенью 2, и определить специальную последовательность
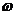 соотношением соотношением
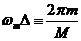 ,
(П.1.4) ,
(П.1.4)
где 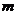 принимает
значения принимает
значения 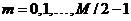 .
Тогда уравнение (П.1.3) принимает форму .
Тогда уравнение (П.1.3) принимает форму
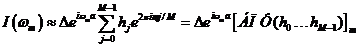 .
(П.1.5) .
(П.1.5)
Несмотря на свою простоту и ясность, использовать
уравнение (П.1.5) не рекомендуется. Оно, как правило, дает неверный
результат!
Проблема заключена в колебательном характере интеграла
(П.1.1). Если
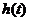 достаточно
гладкая функция и если достаточно
гладкая функция и если 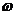 является
достаточно большой, чтобы в интервале является
достаточно большой, чтобы в интервале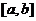 вместилось
несколько циклов – фактически, вместилось
несколько циклов – фактически,
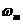 в
уравнении (П.1.4) дает точно в
уравнении (П.1.4) дает точно 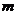 циклов
– тогда значение циклов
– тогда значение 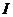 как
правило очень мало, настолько мало, что его значение перекрывается ошибкой
аппроксимации первого порядка и даже второго порядка (при центрированных
значениях). Кроме того, характерным «малым параметром» при оценке ошибки
аппроксимации является не как
правило очень мало, настолько мало, что его значение перекрывается ошибкой
аппроксимации первого порядка и даже второго порядка (при центрированных
значениях). Кроме того, характерным «малым параметром» при оценке ошибки
аппроксимации является не 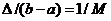 ,
как было бы, если бы подынтегральное выражение не было осциллирующим, а величина ,
как было бы, если бы подынтегральное выражение не было осциллирующим, а величина
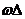 ,
которая может достигать величины ,
которая может достигать величины 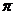 для для
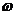 в
пределах частоты Найквиста дискретного преобразования Фурье (сравни уравнение
П.1.4). Это приводит к систематической погрешности в уравнении (П.1.5) по мере
роста в
пределах частоты Найквиста дискретного преобразования Фурье (сравни уравнение
П.1.4). Это приводит к систематической погрешности в уравнении (П.1.5) по мере
роста 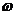 . .
Полезным упражнением является использование уравнения
(П.1.5) для интеграла, который может быть вычислен аналитически, и тогда можно
будет увидеть, насколько плоха такая аппроксимация. Мы рекомендуем читателю
проделать такое упражнение.
Мы же займемся более аккуратным
рассмотрением. Используя данный набор
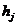 ,
мы можем интерполировать значение ,
мы можем интерполировать значение 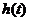 в
любой точке на интервале в
любой точке на интервале 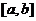 близлежащими
значениями близлежащими
значениями 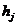 .
Самый простой вариант – линейная интерполяция, использующая два соседних
значения .
Самый простой вариант – линейная интерполяция, использующая два соседних
значения 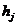 ,
один слева и один – справа. Интерполяцией более высокого порядка могла бы быть,
например, кубическая интерполяция, использующая две точки слева и две – справа -
кроме первого и последнего подинтервалов, в которых мы должны интерполировать
по трем значениям ,
один слева и один – справа. Интерполяцией более высокого порядка могла бы быть,
например, кубическая интерполяция, использующая две точки слева и две – справа -
кроме первого и последнего подинтервалов, в которых мы должны интерполировать
по трем значениям 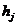 с
одной стороны, одним значением – с другой. с
одной стороны, одним значением – с другой.
Формулами для таких схем интерполяции
являются (кусочные) полиномы относительно независимой переменной
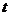 ,
но с коэффициентами, которые линейны по значениям функции ,
но с коэффициентами, которые линейны по значениям функции
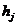 .
Хотя такой подход может быть не является общепринятым, тем не менее интерполяция
нашей функции в любой точке может рассматриваться как приближение функции суммой
базисных функций (которые зависят только от интерполяционной схемы) умноженной
на выборочные значения функции (которые зависят только от функции). Это можно
записать в виде .
Хотя такой подход может быть не является общепринятым, тем не менее интерполяция
нашей функции в любой точке может рассматриваться как приближение функции суммой
базисных функций (которые зависят только от интерполяционной схемы) умноженной
на выборочные значения функции (которые зависят только от функции). Это можно
записать в виде
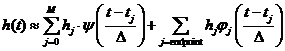 .
(П.1.6) .
(П.1.6)
Здесь
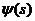 –
базисные функции внутренних точек: Они равны нулю для больших положительных и
отрицательных значений и отличны от нуля только в той области, которая
используется для интерполяции.
Мы всегда имеем –
базисные функции внутренних точек: Они равны нулю для больших положительных и
отрицательных значений и отличны от нуля только в той области, которая
используется для интерполяции.
Мы всегда имеем 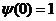 и и
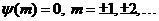 ,
так как интерполяция заданных значений должна дать значение самой функции в этой
точке. Для линейной интерполяции ,
так как интерполяция заданных значений должна дать значение самой функции в этой
точке. Для линейной интерполяции
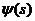 является
кусочно-линейной функцией, значение которой возрастает от 0 до 1 для является
кусочно-линейной функцией, значение которой возрастает от 0 до 1 для
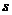 в
интервале (−1, 0), и убывает до 0 для в
интервале (−1, 0), и убывает до 0 для
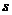 в
интервале (0, 1). Для интерполяции более высокого порядка в
интервале (0, 1). Для интерполяции более высокого порядка
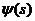 представляет
собой составную кусочную функцию из частей
интерполяционных полиномов Лагранжа. Она имеет разрывные производные при целых
значениях представляет
собой составную кусочную функцию из частей
интерполяционных полиномов Лагранжа. Она имеет разрывные производные при целых
значениях 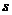 ,
где осуществляется переход с одного набора точек на другой. ,
где осуществляется переход с одного набора точек на другой.
Как уже было отмечено выше, подинтервалы, примыкающие к
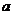 и и
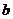 требуют
другой, нецентрированной формулы для интерполяции. Это отражено в уравнении
(П.1.6) второй суммой, со специальными базисными функциями концевых точек.
Фактически, по причинам, которые станут ясными ниже, мы включили в первую сумму
(с базисными функциями) все точки, так что фактически являются разностями между
настоящими концевыми базисными функциями и внутренними базисными функциями требуют
другой, нецентрированной формулы для интерполяции. Это отражено в уравнении
(П.1.6) второй суммой, со специальными базисными функциями концевых точек.
Фактически, по причинам, которые станут ясными ниже, мы включили в первую сумму
(с базисными функциями) все точки, так что фактически являются разностями между
настоящими концевыми базисными функциями и внутренними базисными функциями
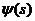 .
Это - утомительное, но полезное упражнение записать весь набор функций .
Это - утомительное, но полезное упражнение записать весь набор функций
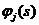 для
любого порядка интерполяции. для
любого порядка интерполяции.
Теперь применим интегральный оператор
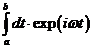 к
обеим частям уравнения (П.1.6), поменяем местами суммирование и интегрирование,
и сделаем замену переменных, введя к
обеим частям уравнения (П.1.6), поменяем местами суммирование и интегрирование,
и сделаем замену переменных, введя 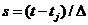 в
первой сумме и в
первой сумме и 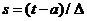 во
второй сумме. В результате получим во
второй сумме. В результате получим
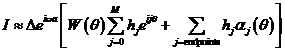 .
(П.1.7) .
(П.1.7)
Здесь
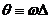 ,
а функции ,
а функции 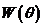 и и
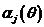 определены
соотношениями определены
соотношениями
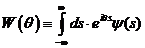 (П.1.8)
(П.1.8)
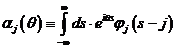 (П.1.9)
(П.1.9)
Ключевым моментом является то, что
интегралы в (П.1.8) и (П.1.9) могут быть вычислены аналитически, раз и навсегда
для любой заданной интерполяционной схемы. Тогда уравнение (П.1.8) может
рассматриваться как алгоритм «коррекции краевых эффектов» для суммы, которая,
как мы видели, может быть вычислена с помощью БПФ, получая тем самым результат с
высокой точностью.
Мы рассмотрим только симметричную интерполяцию.
Симметрия предполагает
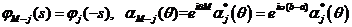 ,
(П.1.10) ,
(П.1.10)
где * обозначает комплексное сопряжение.
Предположение о том, что 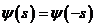 приводит
к утверждению, что приводит
к утверждению, что
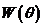 –
действительна. –
действительна.
Вернемся теперь к рассмотрению
суммы в (П.1.7), которую мы хотим вычислить с помощью БПФ. Для этого выберем
некоторое целое 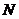 ,
которое является целой степенью 2, так что ,
которое является целой степенью 2, так что
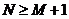 .
(Отметим, что .
(Отметим, что 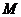 не
должно быть степенью 2, так что не
должно быть степенью 2, так что 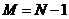 допустимо).
Если допустимо).
Если 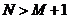 ,
то определим ,
то определим 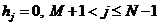 ,
т.е. сделаем нулевую «обкладку» массива ,
т.е. сделаем нулевую «обкладку» массива
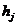 ,
так чтобы ,
так чтобы 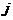 изменялось
в диапазоне изменялось
в диапазоне 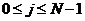 .
После этого сумма может быть вычислена с помощью БПФ для специальных значений .
После этого сумма может быть вычислена с помощью БПФ для специальных значений
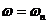 ,
которые вычисляются по формуле ,
которые вычисляются по формуле
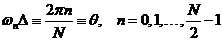 .
(П.1.11) .
(П.1.11)
Чем большее значение
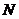 будет
выбрано для заданного будет
выбрано для заданного 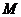 ,
тем более высокие значения
частоты удастся получить, поскольку с увеличением ,
тем более высокие значения
частоты удастся получить, поскольку с увеличением
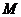 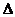 уменьшается
(см. уравнение (П.1.2)), а наибольшее значение уменьшается
(см. уравнение (П.1.2)), а наибольшее значение
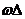 всегда
меньше всегда
меньше 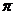 (П.1.11).
Как правило, рекомендуется выбирать множитель на менее 4, т.е. (П.1.11).
Как правило, рекомендуется выбирать множитель на менее 4, т.е.
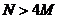 (см.
далее). Мы можем переписать уравнение (П.1.7) в окончательной форме (см.
далее). Мы можем переписать уравнение (П.1.7) в окончательной форме
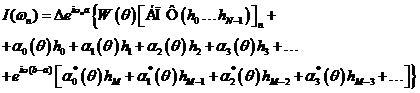 (П.1.12)
(П.1.12)
Для кубической (или более низкого
порядка) полиномиальной интерполяции отличны от нуля только члены, явно
выписанные в (П.1.12), а многоточие можно игнорировать, а для расчетов нам
необходимо явное выражение только для
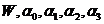 ,
вычисленные с помощью уравнений (П.1.8-П.1.9). Эти выражения вычислены и
приведены в [15]
для второго порядка (формула трапеций) и четвертого порядка (кубическая
интерполяция). Мы переписали программу
DFTCOR,
которая приведена в упомянутом пособии на языке Фортран и
C
на Matlab
и использовали ее в своих расчетах. Описанная процедура корректировки
справедлива для всех значений ,
вычисленные с помощью уравнений (П.1.8-П.1.9). Эти выражения вычислены и
приведены в [15]
для второго порядка (формула трапеций) и четвертого порядка (кубическая
интерполяция). Мы переписали программу
DFTCOR,
которая приведена в упомянутом пособии на языке Фортран и
C
на Matlab
и использовали ее в своих расчетах. Описанная процедура корректировки
справедлива для всех значений 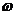 ,
удовлетворяющих условию ,
удовлетворяющих условию 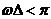 ,
а не только для тех дискретных значений, в которых выполняется БПФ (см. П.1.11),
поэтому для произвольного значения ,
а не только для тех дискретных значений, в которых выполняется БПФ (см. П.1.11),
поэтому для произвольного значения 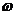 выполняется
полиномиальная интерполяция рассчитанных значений по полученному дискретному
спектру. Для того, чтобы такая интерполяция была достаточно аккуратна,
желательно выполняется
полиномиальная интерполяция рассчитанных значений по полученному дискретному
спектру. Для того, чтобы такая интерполяция была достаточно аккуратна,
желательно
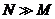 .
Следует также иметь в виду специальное рассмотрение для .
Следует также иметь в виду специальное рассмотрение для
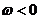 .
Если функция .
Если функция 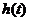 действительна,
то Фурье-образ симметричен относительно действительна,
то Фурье-образ симметричен относительно
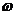 . .
Программа на Matlab, реализующая описанный
алгоритм, помещена здесь Программа быстрого расчета
Фурье-подобных интегралов
Свертки двух непрерывных функций определяется
соотношением
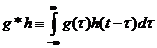 ; ;
Теорема о свертке гласит, что Фурье-образ свертки
двух непрерывных функций равен произведению их индивидуальных Фурье-образов.
Везде далее рассматривается одномерный случай, но это справедливо и для
двумерного случая с соответствующими обобщениями.
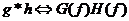 . .
Теперь, имея дело с дискретными величинами,
обсудим как эффективно вычислять ее, используя БПФ. Изложение далее во многом
следует [15], но
поскольку этот источник мало доступен нашему читателю, мы решили включить
основные моменты в нашу работу.
Свертка двух функций
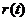 и и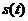 ,
обозначаемая как ,
обозначаемая как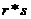 ,
эквивалентна их свертке ,
эквивалентна их свертке 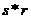 .
Тем не менее, в большинстве приложений эти две функции имеют совершенно
различный смысл. Одна из функций, обычно .
Тем не менее, в большинстве приложений эти две функции имеют совершенно
различный смысл. Одна из функций, обычно
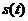 ,
как правило, является сигналом или потоком данных, который изменяется
неограниченно по времени (или по какому-либо другому независимому аргументу).
Другая функция ,
как правило, является сигналом или потоком данных, который изменяется
неограниченно по времени (или по какому-либо другому независимому аргументу).
Другая функция 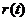 –
«функция отклика», как правило, функция с выраженным пиком, стремящаяся к нулю
по обе стороны от максимума. Действие свертки состоит в том, чтобы «размазать»
сигнал –
«функция отклика», как правило, функция с выраженным пиком, стремящаяся к нулю
по обе стороны от максимума. Действие свертки состоит в том, чтобы «размазать»
сигнал 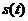 по
времени, в соответствии с формой, заданной функцией отклика по
времени, в соответствии с формой, заданной функцией отклика
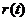 .
В частности, острый пик или дельта-функция единичной площади сигнала .
В частности, острый пик или дельта-функция единичной площади сигнала
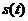 в
какой-либо момент времени в
какой-либо момент времени 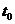 должна
принять форму функции отклика, но сдвинутой по времени с должна
принять форму функции отклика, но сдвинутой по времени с
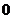 до до
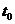 как как
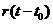 . .
В дискретном случае сигнал
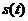 представлен
своими значениями представлен
своими значениями 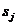 ,
выбранными через равные интервалы времени. Функция отклика также представлена
набором дискретных чисел ,
выбранными через равные интервалы времени. Функция отклика также представлена
набором дискретных чисел 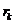 ,
которые интерпретируются следующим образом: ,
которые интерпретируются следующим образом:
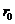 показывает
во сколько раз увеличивается входной сигнал, идущий по какому-либо каналу показывает
во сколько раз увеличивается входной сигнал, идущий по какому-либо каналу
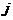 ,
при передаче его в идентичный выходной канал (с таким же номером ,
при передаче его в идентичный выходной канал (с таким же номером
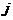 ); );
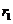 показывает
во сколько раз увеличивается входной сигнал в канале показывает
во сколько раз увеличивается входной сигнал в канале
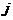 перед
передачей на суммирование в выходной канал перед
передачей на суммирование в выходной канал
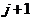 ; ;
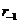 показывает
во сколько раз увеличивается сигнал при передаче на суммирование в канал показывает
во сколько раз увеличивается сигнал при передаче на суммирование в канал
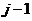 ;
и так далее, как для положительных, так и для отрицательных значений ;
и так далее, как для положительных, так и для отрицательных значений
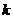 в в
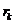 . .
Пример: функция отклика с 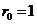 и
всеми другими и
всеми другими 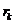 равными
нулю, является тождественным фильтром: свертка сигнала с такой функцией отклика
дает тот же сигнал. Другой пример: функция отклика с равными
нулю, является тождественным фильтром: свертка сигнала с такой функцией отклика
дает тот же сигнал. Другой пример: функция отклика с 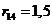 и
всеми остальными и
всеми остальными 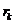 равными
нулю. Результатом свертки будет входной сигнал, умноженный на 1,5 и имеющий
задержку в 14 интервалов выборки. равными
нулю. Результатом свертки будет входной сигнал, умноженный на 1,5 и имеющий
задержку в 14 интервалов выборки.
Очевидно, что мы всего лишь словесно
описали следующее определение дискретной свертки функции отклика конечной
длительности
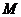 : :
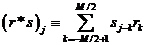 (П.2.1)
(П.2.1)
Если дискретная функция отклика ненулевая на
некотором интервале 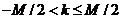 ,
где ,
где
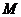 достаточно
большое четное целое, то функция отклика называется «конечный импульсный отклик
(КИО)» , и его длительность есть достаточно
большое четное целое, то функция отклика называется «конечный импульсный отклик
(КИО)» , и его длительность есть
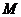 .
(Заметим, что мы определяем .
(Заметим, что мы определяем
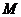 как
число ненулевых значений как
число ненулевых значений 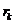 ;
эти значения покрывают временной интервал в ;
эти значения покрывают временной интервал в
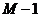 интервалов).
В большинстве практических ситуаций именно конечная интервалов).
В большинстве практических ситуаций именно конечная 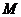 представляет
наибольший интерес, потому что отклик фактически имеет конечную длительность,
или потому, что мы можем обрезать его в любой точке и аппроксимировать его
функцией отклика конечной длительности. представляет
наибольший интерес, потому что отклик фактически имеет конечную длительность,
или потому, что мы можем обрезать его в любой точке и аппроксимировать его
функцией отклика конечной длительности.
Дискретная теорема о свертке гласит: если сигнал
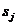 периодичен
с периодом периодичен
с периодом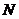 ,
так что он полностью определен ,
так что он полностью определен 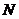 значениями
сигнала значениями
сигнала 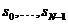 ,
тогда его дискретная свертка с функцией отклика конечной длительности ,
тогда его дискретная свертка с функцией отклика конечной длительности
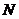 ,
является членом пары образ-прообраз дискретного Фурье-преобразования. ,
является членом пары образ-прообраз дискретного Фурье-преобразования.
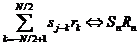 (П.2.2)
(П.2.2)
Здесь
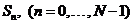 –
дискретное Фурье-преобразование значений –
дискретное Фурье-преобразование значений
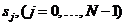 ,
тогда как ,
тогда как 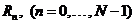 –
дискретное Фурье-преобразование значений –
дискретное Фурье-преобразование значений
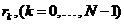 .
Эти значения .
Эти значения 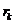 точно
такие же, как и для интервала точно
такие же, как и для интервала 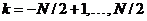 ,
но расположены с циклическим сдвигом. ,
но расположены с циклическим сдвигом.
Дискретная теорема о свертке использует
два предположения, которые не всегда выполняются. Во-первых, предполагается, что
входной сигнал периодичен, тогда как реальные данные часто изменяются во времени
без каких-либо повторений или представляют собой один импульс конечной длины.
Во-вторых, в теореме о свертке предполагается, что длительность отклика равна
периоду входного сигнала, т.е. 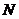 .
Нам нужно как-то преодолеть эти ограничения. .
Нам нужно как-то преодолеть эти ограничения.
Второе ограничение преодолевается очень
просто. Почти всегда представляет интерес функция отклика длительности
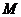 ,
много меньшей, чем длина ряда входных данных ,
много меньшей, чем длина ряда входных данных
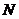 .
В этом случае легко расширить функцию отклика до длины .
В этом случае легко расширить функцию отклика до длины
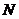 ,
дополняя ее нулями, например, определяя ,
дополняя ее нулями, например, определяя
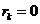 для для
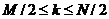 ,
а также для ,
а также для 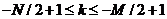 .
Первое ограничение более неудобно. Так как теорема о свертке не очень
обоснованно предполагает, что данные периодичны, то происходит «засорение»
первого выходного канала .
Первое ограничение более неудобно. Так как теорема о свертке не очень
обоснованно предполагает, что данные периодичны, то происходит «засорение»
первого выходного канала 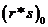 некоторыми
данными (за счет циклического сдвига) с дальнего конца потока данных некоторыми
данными (за счет циклического сдвига) с дальнего конца потока данных
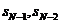 ,
и т.д. Таким образом, нам нужно создать буферное пространство для нулевых
значений на конце вектора ,
и т.д. Таким образом, нам нужно создать буферное пространство для нулевых
значений на конце вектора 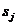 ,
чтобы обнулить эти «засорения». Сколько же нулевых значений должно быть в этом
буфере? Ровно столько, каков наибольший отрицательный индекс, при котором
функция отклика ненулевая. Например, если ,
чтобы обнулить эти «засорения». Сколько же нулевых значений должно быть в этом
буфере? Ровно столько, каков наибольший отрицательный индекс, при котором
функция отклика ненулевая. Например, если
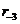 ненулевая,
в то время как ненулевая,
в то время как 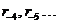 все
равны нулю, то нам нужны три нуля в конце ряда данных: все
равны нулю, то нам нужны три нуля в конце ряда данных:
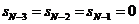 .
Эти нули предохранят первый выходной канал .
Эти нули предохранят первый выходной канал
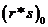 от
«засорений». Совершенно очевидно, что второй выходной канал от
«засорений». Совершенно очевидно, что второй выходной канал
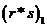 и
последующие предохраняются этими же нулями. Обозначим число конечных нулей и
последующие предохраняются этими же нулями. Обозначим число конечных нулей
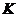 ,
тогда последняя фактическая точка входных данных будет ,
тогда последняя фактическая точка входных данных будет
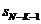 . .
Как устранять «засорения» самого
последнего канала? Так как теперь ряд данных оканчивается членом
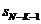 ,
то последний, интересующий нас выходной канал будет ,
то последний, интересующий нас выходной канал будет
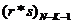 .
Канал может засоряться зацикленными данными из входного канала .
Канал может засоряться зацикленными данными из входного канала
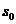 ,
если только число ,
если только число 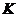 не
будет достаточно большим, т.е таким, чтобы соответствовать наибольшему
положительному индексу не
будет достаточно большим, т.е таким, чтобы соответствовать наибольшему
положительному индексу 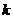 ,
при котором функция отклика ,
при котором функция отклика 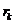 ненулевая.
Например, если от ненулевая.
Например, если от 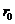 до до
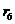 все
ненулевые, тогда как все
ненулевые, тогда как 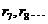 равны
нулю, нам нужно взять по меньшей мере равны
нулю, нам нужно взять по меньшей мере
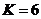 дополнительных
нулей в конце ряда данных: дополнительных
нулей в конце ряда данных: 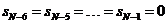 . .
Итак, нам нужно заканчивать ряд данных
нулями на одном конце, число которых равно или максимальной положительной
длительности или максимальной отрицательной длительности функции отклика, в
зависимости от того, какая из них больше. (Для симметричной функции отклика
длительности 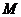 нужно нужно
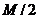 нулей.)
Комбинируя эту операцию с описанным выше способом дополнения нулями отклика нулей.)
Комбинируя эту операцию с описанным выше способом дополнения нулями отклика
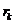 ,
мы можем предохранить данные от нежелательного загрязнения за счет
несуществующей периодичности. ,
мы можем предохранить данные от нежелательного загрязнения за счет
несуществующей периодичности.
Данные, дополненные нулями, представляют
собой ряд вещественных чисел 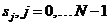 ,
функция отклика ,
функция отклика 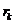 дополнена
нулями до длительности дополнена
нулями до длительности 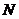 и
проведен циклический сдвиг. (Обычно это означает, что наибольший непрерывный
сегмент и
проведен циклический сдвиг. (Обычно это означает, что наибольший непрерывный
сегмент 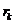 в
середине массива – нулевой, а ненулевые значения сосредоточены на концах
массива). Теперь можно вычислить дискретную свертку следующим образом.
Используйте БПФ-алгоритм для вычисления дискретных Фурье-образов в
середине массива – нулевой, а ненулевые значения сосредоточены на концах
массива). Теперь можно вычислить дискретную свертку следующим образом.
Используйте БПФ-алгоритм для вычисления дискретных Фурье-образов
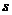 и и
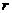 .
Затем нужно перемножить эти два преобразования почленно, помня, что образы
состоят из комплексных чисел. Далее используйте алгоритм БПФ для получения
обратного дискретного Фурье-преобразования произведений. Результатом и будет
свертка .
Затем нужно перемножить эти два преобразования почленно, помня, что образы
состоят из комплексных чисел. Далее используйте алгоритм БПФ для получения
обратного дискретного Фурье-преобразования произведений. Результатом и будет
свертка 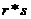 . .
Программа свертки (1-мерной и 2-мерной) на
Matlab |