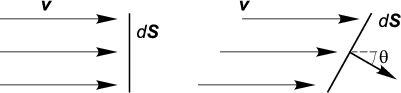5 Теорема Гаусса

§5 Теорема Гаусса

Принцип суперпозиции в сочетании с законом Кулона даёт ключ к вычислению электрического поля произвольной системы зарядов, но непосредственное суммирование полей по формуле (4.2) обычно требует сложных вычислений. Впрочем, при наличии той или иной симметрии системы зарядов вычисления существенно упрощаются, если ввести понятие потока электрического поля и использовать теорему Гаусса.

Представления о потоке электрического поля привнесены в электродинамику из гидродинамики. В гидродинамике поток жидкости через трубу, то есть объём жидкости N, проходящий через сечение трубы в единицу времени, равен v⋅S, где v — скорость жидкости, а S — площадь сечения трубы. Если скорость жидкости изменяется по сечению, нужно использовать интегральную формулу N = ∫ Sv→⋅dS→. Действительно, выделим в поле скоростей малую площадку dS, перпендикулярную к вектору скорости (рис. 1.4).

Рис. 1.4:

Поток жидкости

Объём жидкости, протекающий через эту площадку за время dt, равен v dS dt. Если площадка наклонена к потоку, то соответствующий объём будет v dScosθdt, где θ — угол между вектором скорости v→ и нормалью n→ к площадке dS. Объём жидкости, протекающий через площадку dS в единицу времени получается делением этой величины на dt. Он равен v dS cosθdt, т.е. скалярному произведению v→⋅dS→ вектора скорости v→ на вектор элемента площади dS→ = n→dS. Единичный вектор n→ нормали к площадке dS можно провести в двух прямо противоположных направлениях. одно из них условно принимается за положительное. В этом направлении и проводится нормаль n→. Та сторона площадки, из которой выходит нормаль n→, называется внешней, а та, в которую нормаль n→ входит, — внутренней. Вектор элемента площади dS→ направлен по внешней нормали n→ к поверхности, а по величине равен площади элемента dS = ∣dS→∣. При вычислении объёма протекающей жидкости через площадку S конечных размеров, её надо развить на бесконечно малые площадки dS, а затем вычислить интеграл ∫ Sv→⋅dS→ по всей поверхности S.

Выражения типа ∫ Sv→⋅dS→ встречаются во многих отраслях физики и математики. Они называются потоком вектора v→ через поверхность S независимо от природы вектора v→. В электродинамике интеграл

N = ∫ SE→⋅dS→

(5.1)

называют потоком напряженности электрического поля E→ через произвольную поверхность S, хотя с этим понятием не связано никакое реальное течение.

Допустим, что вектор E→ представляется геометрической суммой

E \to = \sum j E \to j .

Умножив это равенство скалярно на dS→ и проинтегрировав, получим

N = \sum j N j .

где Nj — поток вектора E→j через ту же самую поверхность. Таким образом, из принципа суперпозиции напряженности электрического поля следует, что потоки через одну и ту же поверхность складываются алгебраически.

Теорема Гаусса гласит, что поток вектора E→ через произвольную замкнутую поверхность равен умноженному на 4π суммарному заряду Q всех частиц, находящихся внутри этой поверхности:

∮ SE→⋅dS→ = 4πQ.

(5.2)

Вектор элемента поверхности dS→ здесь направлен по нормали, внешней по отношению к тому объему, где сосредоточен заряд Q (рис. 1.5).

Рис. 1.5:

Теорема Гаусса для одного точечного заряда

Доказательство теоремы проведем в три этапа.

1. Начнем с вычисления потока электрического поля одного точечного заряда q (рис. 1.5). В простейшем случае, когда поверхность интегрирования S является сферой, а заряд находится в её центре, справедливость теоремы Гаусса практически очевидна. На поверхности сферы напряженность электрического поля

E \to = q r \to ∕ r 3

постоянна по величине и всюду направлена по нормали к поверхности, так что поток электрического поля просто равен произведению E = q∕r2 на площадь сферы S = 4πr2. Следовательно, N = 4πq. Этот результат не зависит от формы поверхности, окружающей заряд. Чтобы доказать это, выделим произвольную площадку поверхности достаточно малого размера с установленным на ней направлением внешней нормали n→. На рис. 1.6 показан один такой сегмент преувеличенно большого (для наглядности) размера.

Рис. 1.6:

Поток электрического в элемент телесного угла

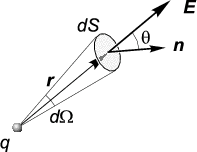
Поток вектора E→ через эту площадку равен

d N = E \to \cdot d S \to = E cos θ d S,

где θ — угол между направлением E→ и внешней нормалью n→ к площадке dS. Так как E = q∕r2, а dScosθ∕r2 по абсолютной величине есть элемент телесного угла dΩ = dS∣cosθ∣∕r2, под которым видна площадка dS из точки расположения заряда,

d N = \pm q d Ω .

где знаки плюс и минус отвечают знаку cosθ, а именно: следует взять знак плюс, если вектор E→ составляет острый угол с направлением внешней нормали n→, и знак минус в противном случае.

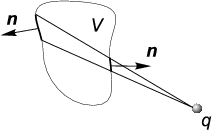
2. Теперь рассмотрим конечную поверхность S, охватывающую некоторый выделенный объём V . По отношению к этому объёму всегда можно определить, какое из двух противоположных направлений нормали к любому элементу поверхности S следует считать внешним. Внешняя нормаль направлена из объёма V наружу. Суммируя по сегментам, с точностью до знака имеем N = q Ω, где Ω — телесный угол, под которым видна поверхность S из точки, где находится заряд q. Если поверхность S замкнута, то Ω = 4π при условии, что заряд q находится внутри S. В противном случае Ω = 0. Чтобы пояснить последнее утверждение, можно вновь обратиться к рис. 1.7.

Рис. 1.7:

Потоки через площадки, опирающиеся на один телесный угол, но обращенные в разные стороны, взаимно сокращаются.

Очевидно, что потоки через сегменты замкнутой поверхности, опирающиеся на равные телесные углы, но обращенные в противоположные стороны, взаимно сокращаются. Очевидно также, что если заряд находится вне замкнутой поверхности, то любому сегменту, обращенному наружу, найдется соответствующий сегмент, обращенный внутрь.

3. Наконец, воспользовавшись принципом суперпозиции, приходим к итоговой формулировке теоремы Гаусса (5.2). Действительно, поле системы зарядов равно сумме полей каждого заряда в отдельности, но в правую часть теоремы (5.2) дают ненулевой вклад только заряды, находящиеся внутри замкнутой поверхности. Этим завершается доказательство.

В макроскопических телах число носителей заряда столь велико, что дискретный ансамбль частиц удобно представить в виде непрерывного распределения, введя понятие плотности заряда. По определению, плотностью заряда ρ называется отношение ΔQ∕ΔV в пределе, когда объём ΔV стремится к физически бесконечно малой величине:

ρ = limΔV →0ΔQ ΔV = dQ dV .

(5.3)

Физически бесконечно малым является объём, который мал по сравнению с любыми другими макроскопическими размерами рассматриваемой задачи, но достаточно велик по сравнению с расстоянием между частицами, в данном случае заряженными частицами. С помощью плотности заряда теорему Гаусса можно переписать в виде

∮ SE→⋅dS→ = 4π ∫ V ρdV ,

(5.4)

где интегрирование в правой части производится по объему V , замкнутому поверхностью S.

Теорема Гаусса даёт одно скалярное уравнение на три компоненты вектора E→, поэтому для расчета электрического поля одной этой теоремы недостаточно. Необходима известная симметрия распределения плотности зарядов, чтобы задача могла быть сведена к одному скалярному уравнению. Теорема Гаусса позволяет найти поле в тех случаях, когда поверхность интегрирования в (5.4) удается выбрать так, что напряженность электрического поля E постоянна на всей поверхности. Рассмотрим наиболее поучительные примеры.

▸Задача 5.1

Найти поле шара, равномерно заряженного по объёму или поверхности.

Решение: Электрическое поле точечного заряда E→ = q r→∕r3 стремится к бесконечности при r → 0. Этот факт показывает противоречивость представления элементарных частиц точечными зарядами. Если же заряд q равномерно распределен по объему шара конечного радиуса a, то электрическое поле не имеет особенностей.

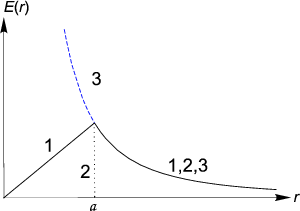
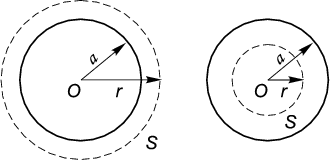
Из симметрии задачи ясно, что электрическое поле E→ всюду направлено радиально, а его напряженность E = E(r) зависит только от расстояния r до центра шара. Тогда поток электрического поля через сферу радиуса r просто равен 4πr2E (рис. 1.8).

Рис. 1.8:

Вычисление поля симметрично заряженного шара с помощью теоремы Гаусса

С другой стороны, заряд внутри той же сферы равен полному заряду шара Q, если r ≥ a. Приравнивая 4πr2E к умноженному на 4π заряду шара q, получаем:

E (r) = q ∕ r 2 .

Таким образом, во внешнем пространстве заряженный шар создает такое поле, как если бы весь заряд был сосредоточен в его центре. Этот результат справедлив при любом сферически симметричном распределении заряда.

Поле внутри шара равно E(r) = Q∕r2, где Q — заряд внутри серы радиуса r. Если заряд равномерно распределен по объему шара, то Q = q (r∕a)3. В этом случае

E (r) = q r ∕ a 3 = (4 π ∕ 3) ρ r,

где ρ = q∕(4πa3∕3) — плотность заряда. Внутри шара поле линейно спадает от максимального значения на поверхности шара до нуля в его центре (рис. 1.8).

Рис. 1.9:

Поле равномерно шара, равномерно заряженного по объёму (1), по поверхности (2), и поле точечного заряда той же величины.

Функция E(r) при этом всюду конечна и непрерывна.

Если заряд распределен по поверхности шара, то Q = 0, а поэтому также E = 0. Это результат также справедлив для случая, когда внутри сферической полости зарядов нет, а внешние заряды распределены сферически симметрично. ▸Задача 5.2

Найти поле равномерно заряженной бесконечной нити; радиус нити a, заряд на единицу длины ϰ.

▸Задача 5.3

Найти поле бесконечной прямой нити и бесконечно длинного равномерно заряженного цилиндра.

▸Задача 5.4

Найти поле бесконечной заряженной плоскости и равномерно заряженного бесконечного плоского слоя.

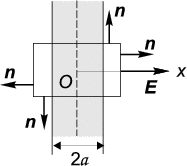
Решение: Вследствие симметрии задачи поле направлено по нормали к слою и зависит только от расстояния x от плоскости симметрии пластины. Для вычисления поля с помощью теоремы Гаусса удобно выбрать поверхность интегрирования S в виде параллелипипеда, как показано на рис. 1.10.

Рис. 1.10:

Вычисление поля плоского слоя с помощью теоремы Гаусса

Тогда отличен от нуля только интеграл по двум противоположным граням параллелипипеда, параллельным слою. Рассуждая, как в предыдущей задаче, найдем:

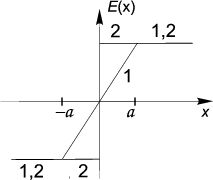
E (x) = - 4 π ρ a при x \leq - a, 4 π ρ x при ∣ x ∣ \leq a, 2 π ρ a при x \geq a .

Вне слоя поле однородно (не зависит от x) и совпадает с полем бесконечной плоскости (рис. 1.11): E(x) = −2πσ при x < 0, E(x) = +2πσ при x > 0.

Рис. 1.11:

Поле бесконечного плоского слоя (1) и бесконечной плоскости (2).

Последний результат получается предельным переходом a → 0 при одновременном увеличении плотности заряда ρ так, чтобы величина σ = ρa оставалась неизменной. По разные стороны от плоскости напряженность электрического поля одинакова по величине, но противоположна по направлению. Поэтому при переходе через заряженную плоскость поле скачком меняется на величину 4πσ. Заметим, что пластина может считаться бесконечной, если расстояние от пренебрежимо мало по сравнению с её размерами. На расстояниях очень больших по сравнению с размерами пластины она действует, как точечный заряд, и её поле убывает обратно пропорционально квадрату расстояния.

[next] [prev] [prev-tail] [front] [up]