Комплексная плоскость

Для множества вещественных чисел $\mathbb R$ используется простая геометрическая интерпретация: числовая прямая.

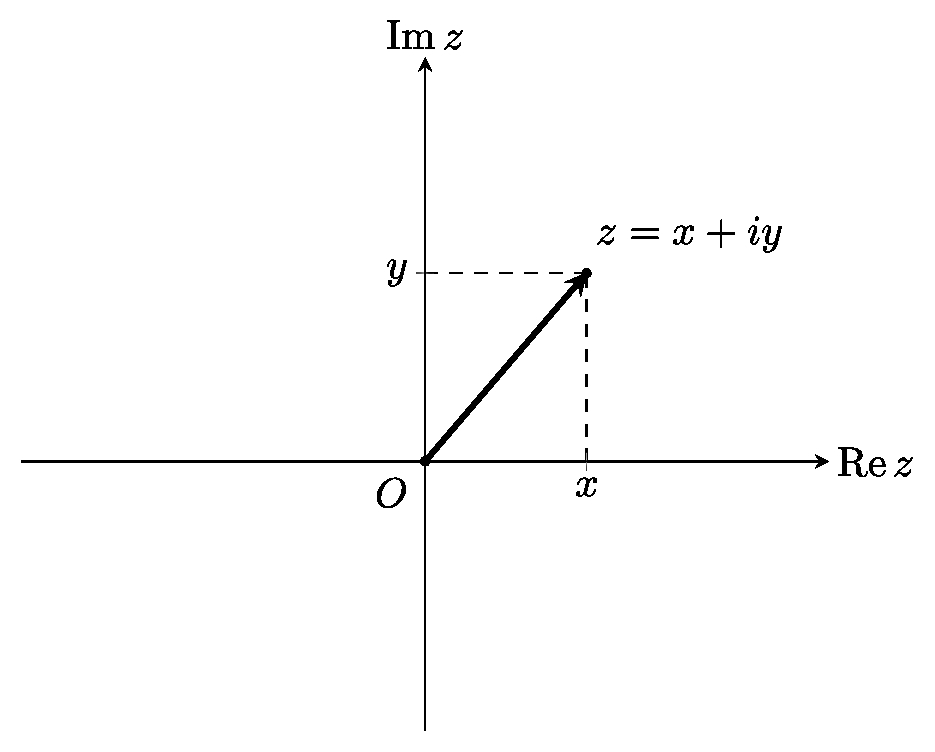
Для множества комплексный чисел геометрический подход оказывается ещё более плодотворным. Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс обозначим $\operatorname{Re} z$ и будем называть действительной осью, а ось ординат обозначим $\operatorname{Im} z$, будем называть мнимой осью. Каждому комплексному числу $z=x+iy$ сопоставим точку на этой плоскости с координатами $(x,y)$, и, другими словами, радиус-вектор с координатами $(x,y)$.

Заметим, что соответствие между комплексными числами и точками на комплесной плоскости является взаимнооднозначным соответствием (а в случае с вещественными числами, соответствие строится с точкам на вещественной прямой).

Модуль комплексного числа $z=x+iy$ равен длине вектора, соответствующего данному числу на комплексной плоскости, $$|z|= \sqrt{x^2+y^2}.$$ Несложно проверить, что расстояние между двумя точками комплексной плоскости $z_1$ и $z_2$ равно $|z_1-z_2|$. То есть, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которым соответствуют этим числам.

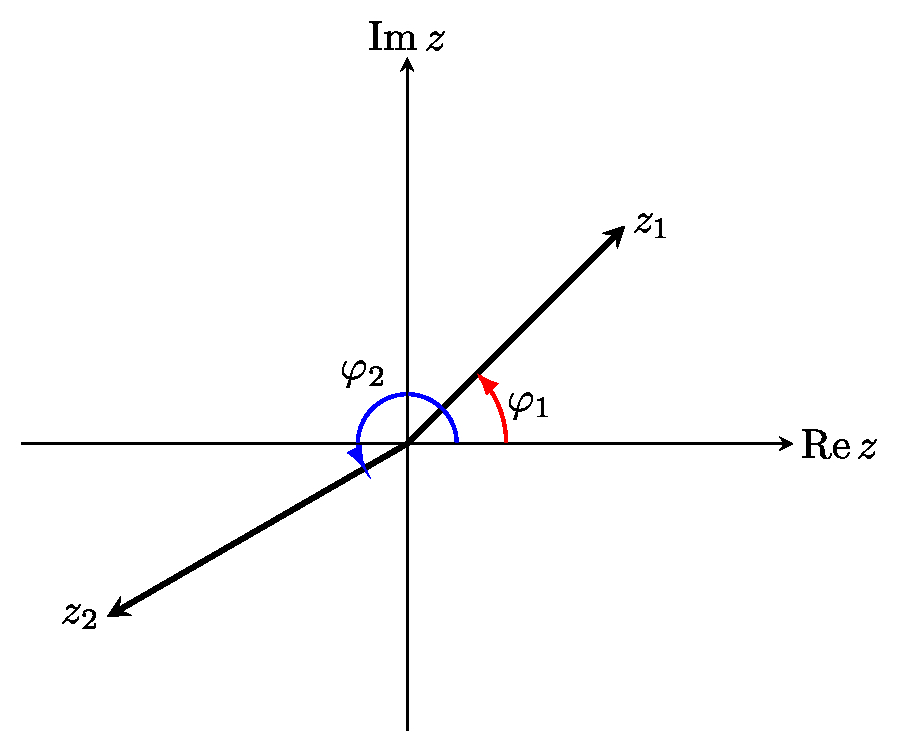
Определение. Аргументом комплексного числа $z=x+iy$ называется угол $\varphi$ между вектором $(x,y)$ и положительным направлением действительной оси $\operatorname{Re} z$ измеряемый против хода часовой стрелки.
Аргумент числа $z$ обозначается $\operatorname{Arg} z$.

Строго говоря, аргумент комплексного числа определен не однозначно, в общем виде аргумент можно записать как $$ \operatorname{Arg} z = \arg z + 2\pi k ,\text{ где } k\in\mathbb Z, $$ где $\arg z$ - главное значение аргумента, $0\leqslant \arg z <2\pi$.
Таким образом, главное значение аргумента комплексного числа определено однозначно .

Единственное комплексное число, для которого значение аргумента не определяют, это $z=0$. Впрочем, это также единственное число, у которого модуль равен нулю, поэтому неопределённость аргумента в данном случае не является проблемой.
Также можно отметить: для действительных чисел $\arg z=0$, если число положительное, и $\arg z = \pi$, если число отрицательное.

Геометрически сложение чисел $z_1$ и $z_2$ производится по правилу сложения векторов (по правилу параллелограмма).

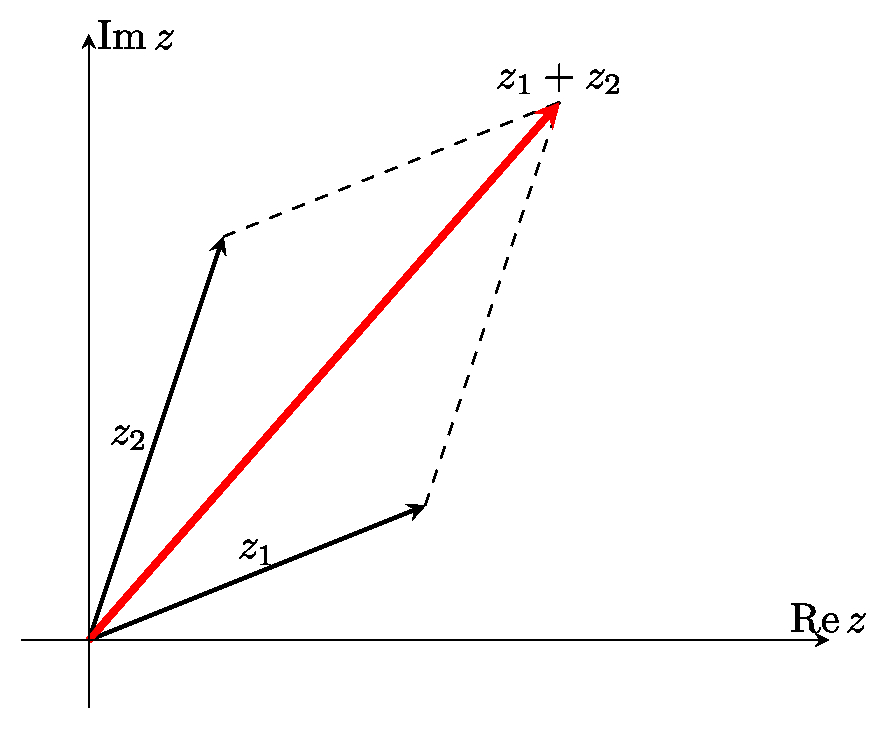
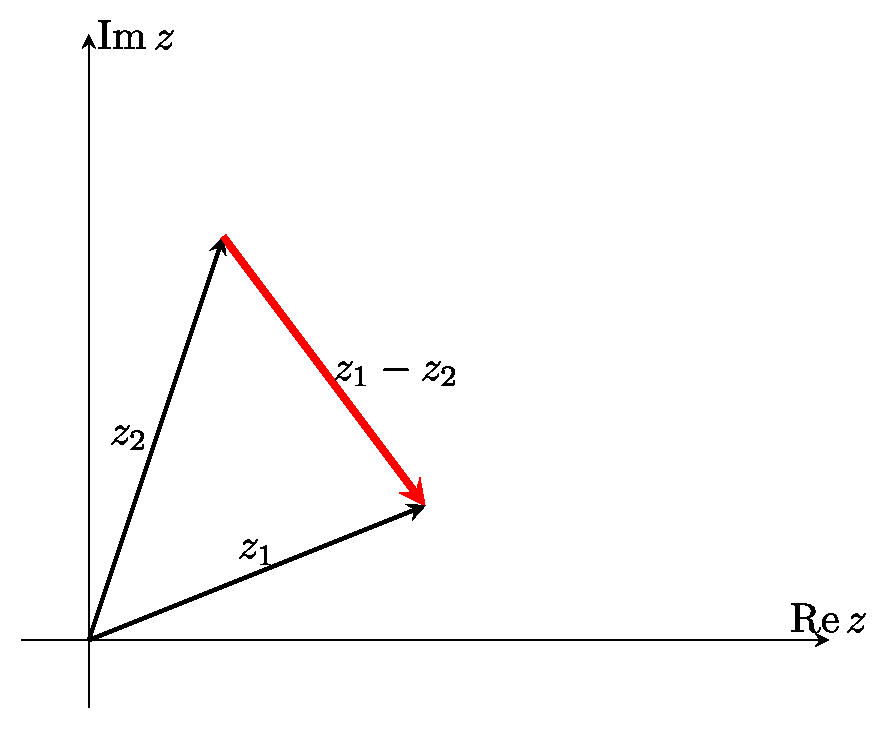
Разность $z_1-z_2$ представляется вектором, конец которого находится в точке $z_1$, а начало --- в точке $z_2$.

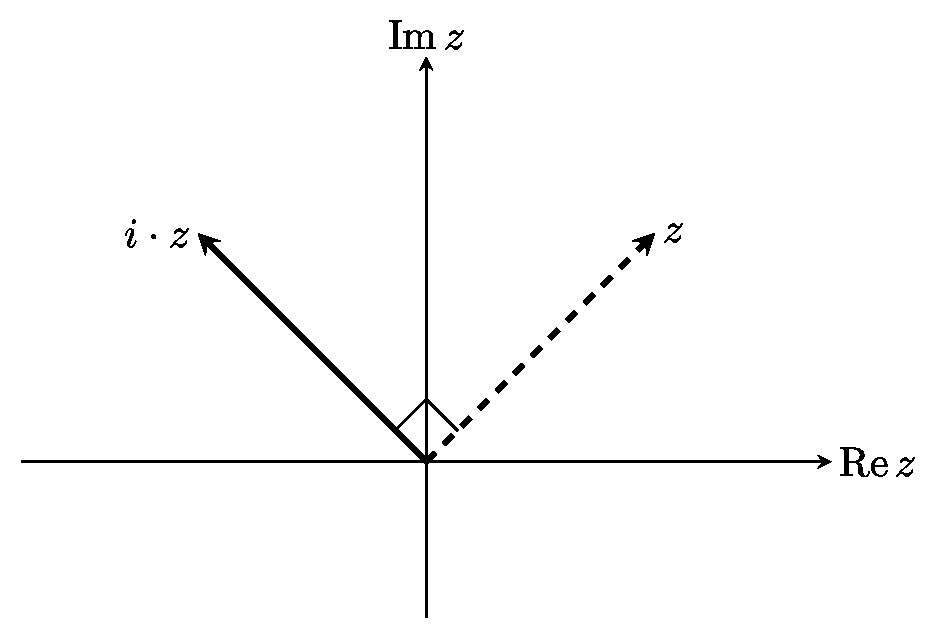
Геометрический смысл умножения на мнимую единицу $i$ состоит в повороте на угол $\pi/2$. Действительно, пусть $z=x+iy$, тогда $i\cdot z = -y + ix$. Преобразование $(x,y)\mapsto(-y,x)$ --- это поворот вектора $(x,y)$ на $\pi/2$ против часовой стрелки.

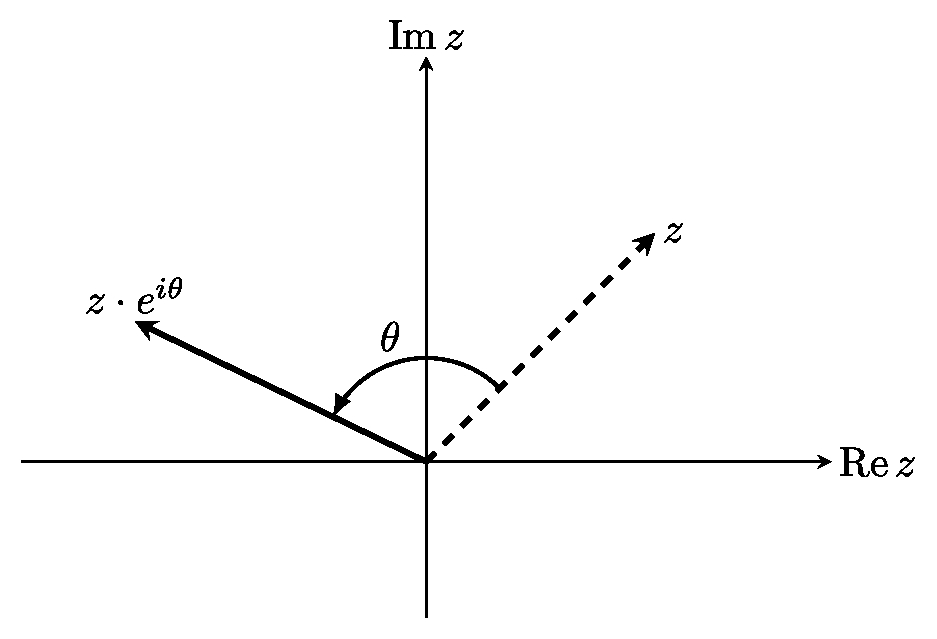
Умножение комплексного числа $z=x+iy$ на комплексную экспоненту $e^{i\theta}$ соответстует повороту на угол $\theta$ против часовой стрелки.

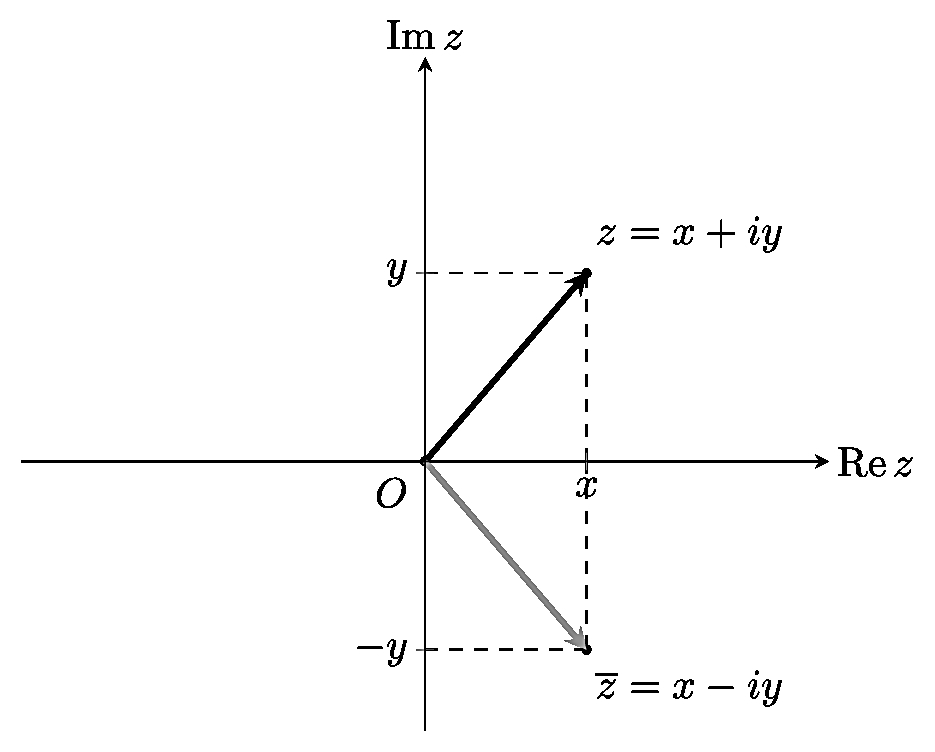
Комплексным сопряжением числа $z$ на комплексной плоскости является вектор, симметричный вектору $z$, относительно оси абсцисс.

В качестве несложного упражнения, изобразите как на комплексной плоскости будет выглядеть вектор $-z$.