Тригонометрическая запись

Пусть $z=x+iy$ и $\varphi = \operatorname{Arg} z$, тогда \begin{equation}\label{eq:cossin} \cos\varphi = \frac{x}{\sqrt{x^2+y^2}}, \quad \sin\varphi = \frac{y}{\sqrt{x^2+y^2}}. \end{equation} Обозначим $\rho = \sqrt{x^2+y^2}$. Из \eqref{eq:cossin} выводим \begin{equation}\label{eq:ReIm} \operatorname{Re} z = x = \rho\cos\varphi \quad\text{ и }\quad \operatorname{Im} z = y = \rho\sin\varphi. \end{equation} В итоге из \eqref{eq:ReIm} имеем \begin{equation}\label{eq:trig_forma} z = \rho(\cos\varphi+i\sin\varphi). \end{equation}

Запись \eqref{eq:trig_forma} называется тригонометрической формой комплексного числа, где $\rho=|z|$, а $\varphi = \operatorname{Arg} z$.

Например, найдём число $z=1+i$ в тригонометрической форме.
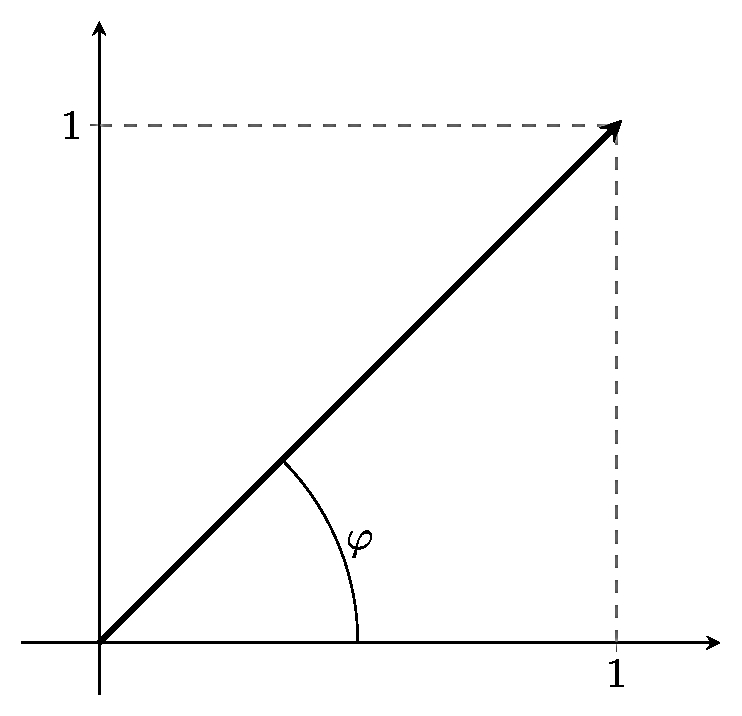Данное число $z$ на комплексной плоскости является вектором с координатами $(1,1)$. Вектор направлен по диагонали единичного квадрата, и поэтому угол $\varphi=\pi/4$. Длина вектора (модуль $z$) $\rho = \sqrt{1+1} = \sqrt{2}$. Таким образом, $$z=\sqrt{2}(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}).$$

Нетрудно заметить, что умножение и деление в тригонометрической форме принимает следующий простой вид \begin{equation*} z_1\cdot z_2 = \rho_1\cdot\rho_2(\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2)), \end{equation*} \begin{equation*} \frac{z_1}{z_2} = \frac{\rho_1}{\rho_2}(\cos(\varphi_1-\varphi_2)+i\sin(\varphi_1-\varphi_2)). \end{equation*} Но тогда для любого целого числа ($k \in\mathbb Z$) верно \begin{equation*} z^k = \rho^k(\cos k\varphi+i\sin k\varphi). \end{equation*} Из чего выводим Формулу Муавра \begin{equation*} (\cos\varphi+i\sin\varphi)^k = \cos k\varphi+i\sin k\varphi. \end{equation*}

Если $z\ne0$, то существует $n$ различных корней $n$-й степени из числа $z$ и их можно найти по следующей формуле: \begin{equation*} w_k = \sqrt[n]{|z|}(\cos\frac{\varphi+2\pi k}{n} + i\sin\frac{\varphi+2\pi k}{n}), \end{equation*} где $k=0,1,2,\dots, n-1$ и $\varphi = \arg z$.