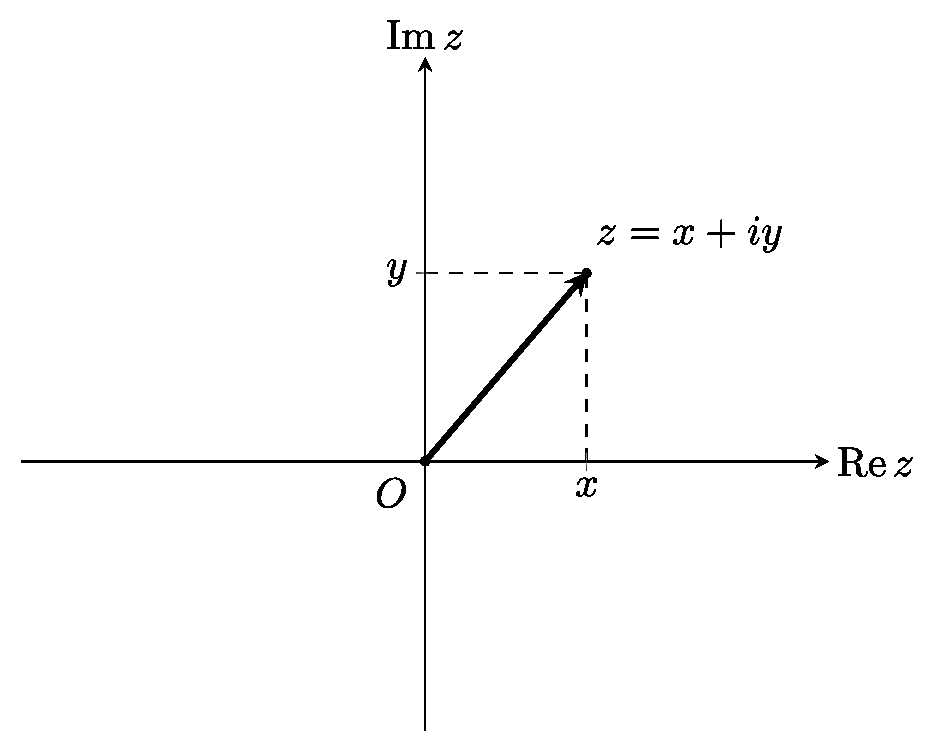
Комплексная плоскость

Для множества вещественных чисел $\mathbb R$ используется простая геометрическая интерпретация: числовая прямая.

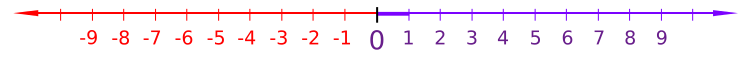
Для множества комплексный чисел геометрический подход оказывается ещё более плодотворным. Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс обозначим $\operatorname{Re} z$ и будем называть действительной осью, а ось ординат обозначим $\operatorname{Im} z$, будем называть мнимой осью. Каждому комплексному числу $z=x+iy$ сопоставим точку на этой плоскости с координатами $(x,y)$, и, другими словами, радиус-вектор с координатами $(x,y)$.