Комплексные функции

Любая функция комплексного переменного может быть записана в виде $$ f(x+iy) = u(x,y) + iv(x,y). $$

Фактически, комплексная функция - это отображение $f:\mathbb R^2 \to \mathbb R^2$. Стало быть, можно использовать технику многомерного математического анализа. В первую очередь это относится к пределу и непрерывности функции. Однако понятие комплексной дифференцируемости отличается от дифференцируемости на плоскости.

Графическое представление

В общем случае для комплексной функции нельзя построить привычный нам график, так он является множеством в $\mathbb R^4$. Существует несколько подходов к графическому представлению комплексной функции.

• Изображение отдельных компонент

  Отдельно можно строить графики аргумента и модуля функции, понимая $\operatorname{arg} f(z)$ и $|f(x)|$ как вещественные функции двух переменных. Ниже приведён пример графика модуля синуса.

Метод цветных областей

Идея состоит в том, чтобы закодировать значение $\operatorname{arg} f(z)$ цветом, а $|f(z)|$ яркостью.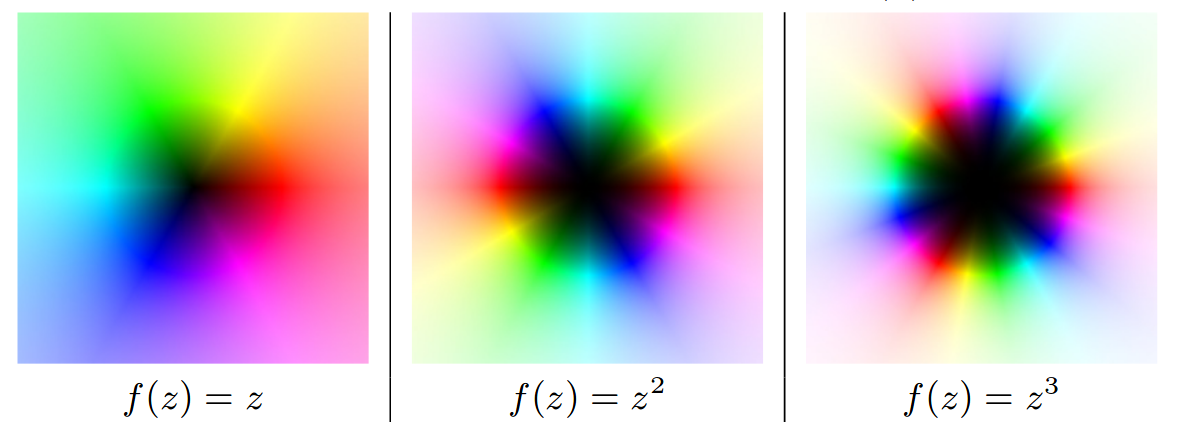

Попробывать метод цветных областей ⇢

Преобразование плоскости

Можно отслеживать во что переходят различные фигуры под действием функции. На рисунке ниже функция $f(z) = (1+i\sqrt{3})z$.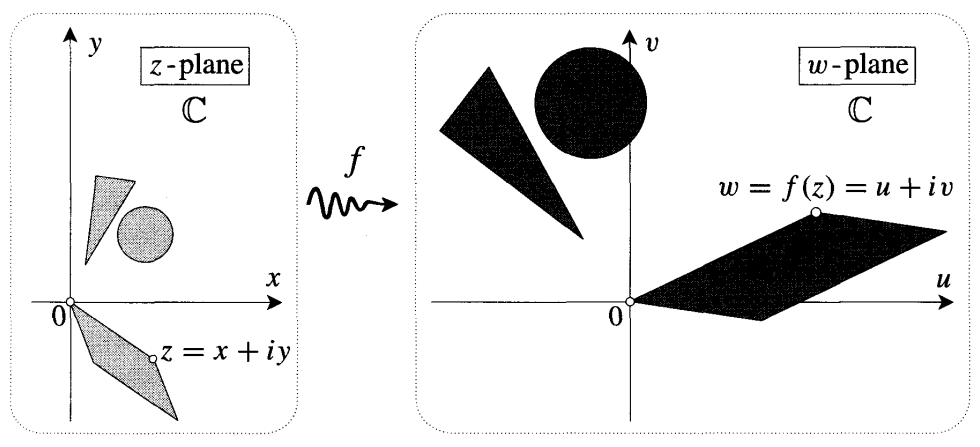

Комплексная производная

Пусть $\Omega\subset\mathbb C$ - открытое множество и $z_0\in \Omega$. Функция $f:\Omega\to\mathbb C$ называется дифференцируемой в точке $z_0$, если существует предел $$ \lim\limits_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0} = f'(z_0). $$ Эквивалентное определение дифференцируемости в точке $z_0$: существует константа $\lambda\in\mathbb C$ такая, что $$ f(z) = f(z_0) + \lambda(z-z_0) + o(|z-z_0|). $$