Элементы теории вычетов
Вычетом функции $f(z)$ в изолированной особой точке $z_0\in \mathbb C$ называется величина $$\Res\limits_{z=z_0} f(z) = \frac{1}{2\pi i} \int\limits_{\gamma} f(z)\, dz \quad \text{ или } \quad \Res\limits_{z=z_0} f(z)= c_{-1}.$$
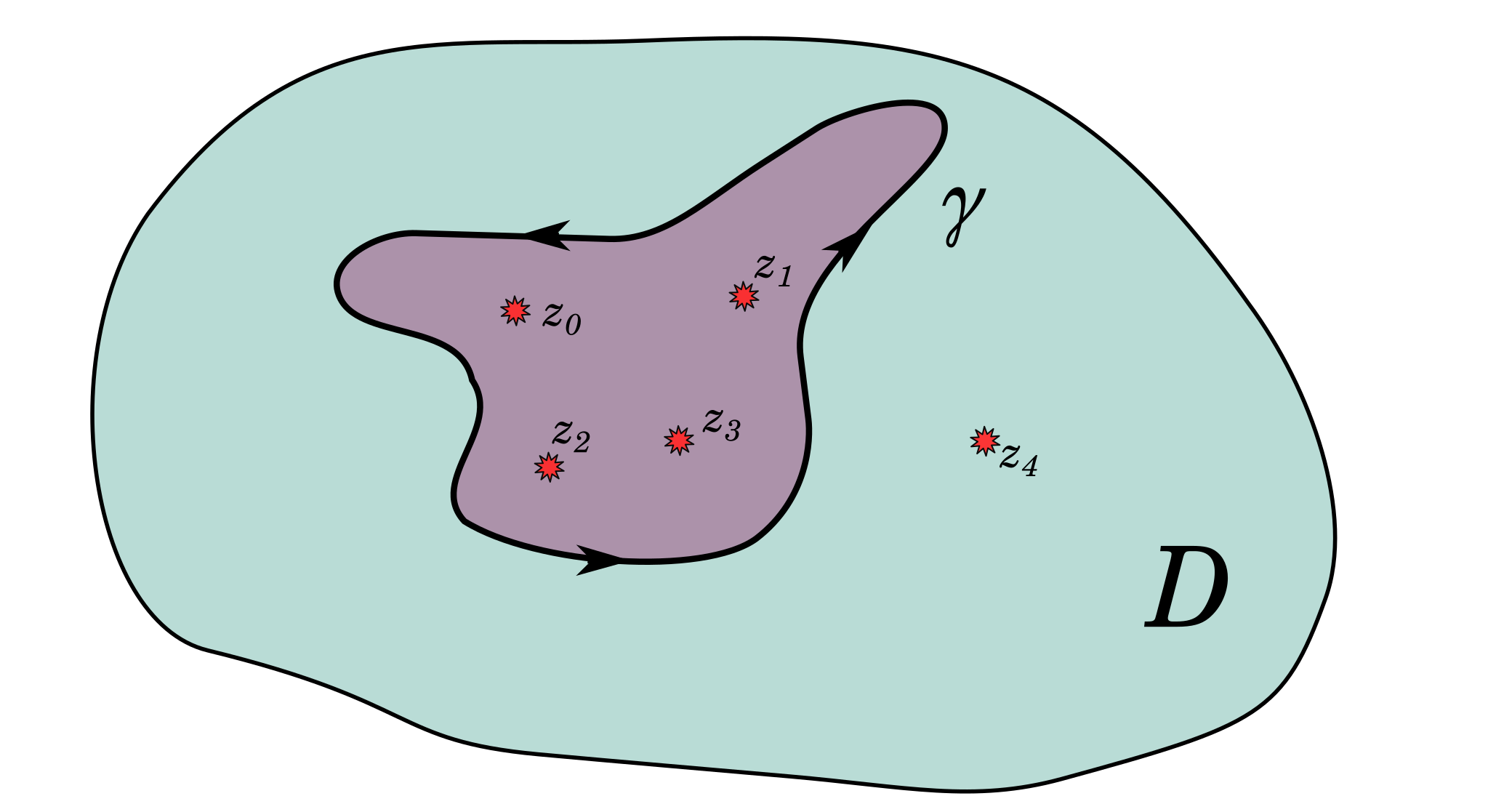
Основная теорема теории вычетов. Пусть $f$ - голоморфна в $D\subset\mathbb C$, за исключением изолированных особых точек $\{z_j\}$, $\gamma$ - простая замкнутая кусочно-гладкая кривая, не содержащая особых точек $\{z_j\}$. Тогда $$ \int\limits_{\gamma} f(z)\, dz = 2\pi i\sum\limits_j\Res\limits_{z=z_j} f(z), $$ где суммирование ведётся по всем точкам $z_j$, находящимся внутри.