Ряды Тейлора и Лорана
Теорема Тейлора. Пусть функция $f$ - аналитична в круге $B(z_0,R)$. Тогда $f$ может быть представлена в $B(z_0,R)$ степенным рядом с центром в $z_0$ (с радиусом сходимости $\geq R$): $$ f(z) = \sum\limits_{k=0}^{\infty}c_k(z-z_0)^k, \qquad c_k = \frac{1}{2\pi i} \int\limits_{\gamma} \frac{f(w) \, dw}{(w-z_0)^{k+1}}. $$ $\gamma\subset B(z_0,R)$ - простой кусочно-гладкий контур, содержащий $z_0$ внутри.
Пример разложения в ряд Тейлора функции $e^{z}$.
Точка $z_0\in\mathbb C$ называется нулём функции $f(z)$, если ${f(z_0) = 0}$.
Классификация нулей.
Пусть $f(z)$ --- аналитическая функция и точка $z_0\in\mathbb C$ является её нулём ($f(z_0)=0$).
Тогда возможны два случая:
1) $f(z)=0$ для всех $z\in B(z_0,\rho)$ для некоторого $\rho>0$
либо
2) существует $m\in\mathbb N$ и аналитическая функция $g(z)$ такая, что $f(z) = (z-z_0)^{m}\cdot g(z)$ и
$g(z_0)\ne0$.
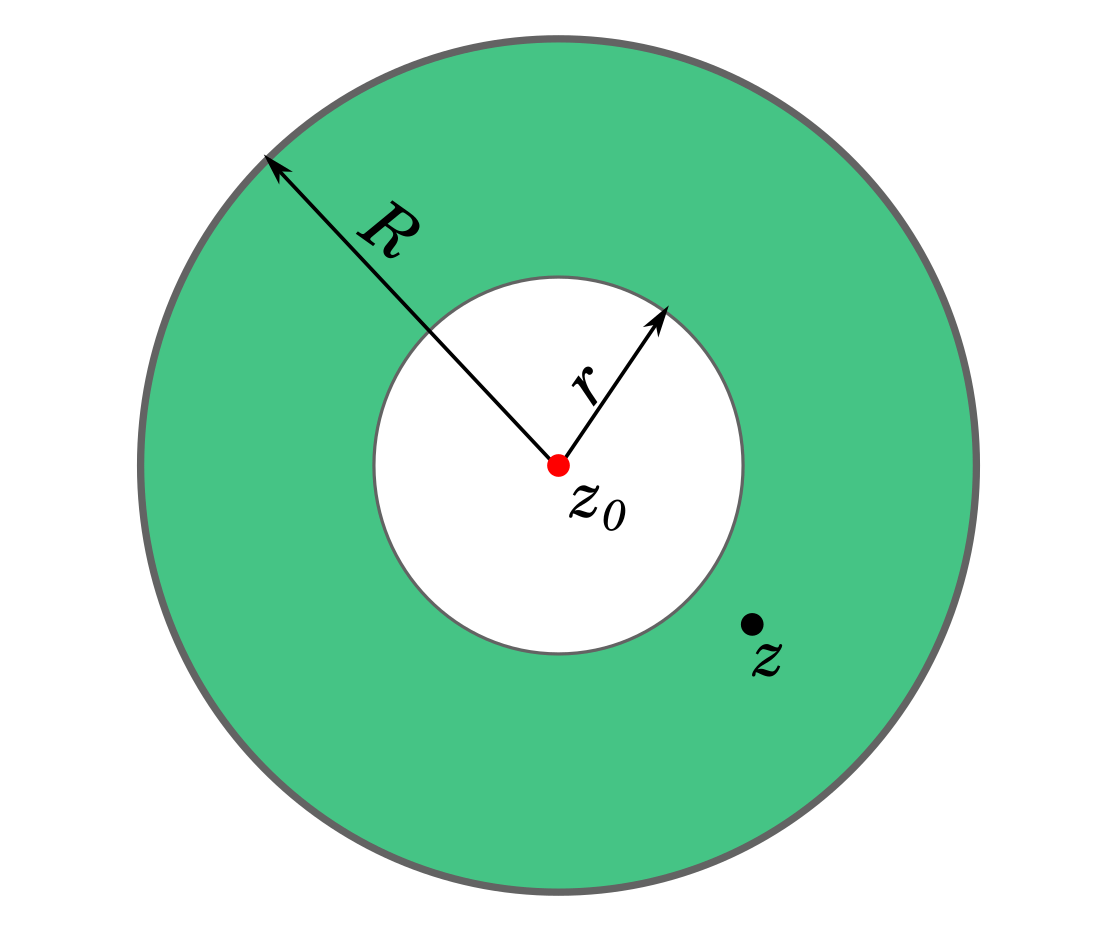
Ряд Лорана
Теорема Лорана. Аналитическая в кольце $K=\{r<|z-z_0|<R\}$ функция $f(z)$ в каждой точке $z\in K$ представима в виде ряда $$ f(z)=\sum\limits_{k=-\infty}^{\infty} c_k (z-z_0)^k, $$ $$ c_k=\frac{1}{2\pi i}\int\limits_{\gamma} \frac{f(w)\,dw}{(w-z_0)^{k+1}}, $$ где $\gamma\subset K$ - простой кусочно-гладкий контур, обходящий точку $z_0$.