Функция Жуковского [док.]
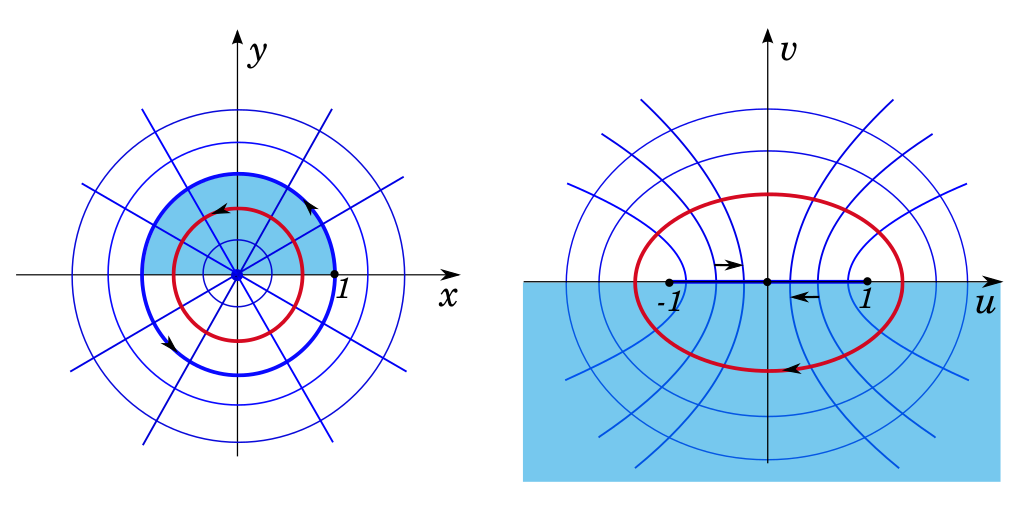
Найти преобразование полярной сетки $|z| = R, \arg z = \alpha$ под действием функции $f(z) = \frac{1}{2}\left(z+\frac{1}{z}\right)$.
Решение
Шаг 1. Записать функцию $f$ в полярных координатах.
Используя тригонометрическое представление $z=r(\cos\varphi + i\sin\varphi)$, отображение можно записать в виде \begin{multline*} w = \frac{1}{2}\left(r(\cos\varphi + i\sin\varphi) + \frac{1}{r(\cos\varphi + i\sin\varphi)}\right)=\\= \frac{1}{2}\left(r(\cos\varphi + i\sin\varphi) + \frac{1}{r}(\cos\varphi - i\sin\varphi)\right). \end{multline*} Тогда \begin{equation}\label{eq:juc2} u = \frac{1}{2}\left(r+\frac{1}{r}\right)\cos\varphi, \qquad v = \frac{1}{2}\left(r-\frac{1}{r}\right)\sin\varphi. \end{equation}
Шаг 2. Найти образ окружности $|z|=R<1$.
Из \eqref{eq:juc2} имеем $$ u = \frac{1}{2}\left(R+\frac{1}{R}\right)\cos\varphi, \quad v = -\frac{1}{2}\left(\frac{1}{R}-R\right)\sin\varphi, \qquad \varphi\in[0,2\pi] $$ — параметрическое уравнение эллипса с полуосями $a=\frac{1}{2}\left(R+\frac{1}{R}\right)$ и $b=\frac{1}{2}\left(\frac{1}{R}-R\right)$. Отметим, что если точка $z$ пробегает окружность $|z|=R$ против часовой стрелки, то точка $w=u+iv$ пробегает этот эллипс по часовой стрелке. При $R\to 1$ эллипс стягивается в отрезок $[-1,1]$.
Шаг 3. Найти образ окружности $|z|=R>1$.
Аналогично получаем, что окружность $|z|=R>1$ преобразуется в эллипс с полуосями $a=\frac{1}{2}\left(R+\frac{1}{R}\right)$ и $b=\frac{1}{2}\left(\frac{1}{R}-R\right)$. Но на этот раз эллипс ориентирован против часовой стрелки.
Шаг 4. Найти образ лучей $\arg z = \alpha$.
Лучи $\arg z = \alpha$ ($\alpha\ne\frac{\pi k}{2}$) переходят ветви гиперболы $$ \dfrac{u^2}{\cos^2\alpha} - \dfrac{v^2}{\sin^2\alpha} = 1. $$ Итак, окружностям $|z| = R$ соответствуют софокусные эллипсы $$ \dfrac{4u^2}{(R + 1/R)^2} + \dfrac{4v^2}{(R - 1/R)^2} = 1 $$ (окружности $|z| = 1$ - отрезок $v =0, -1\leq u \leq 1$). Лучам соответствуют софокусные гиперболы (лучу $\arg z = 0$ - луч $v = 0, u\geq 1,$ лучу $\arg z = \pi$ - луч $v = 0, u\leq -1;$ лучам $\arg z = \pm \pi/2$ - ось $u = 0$).