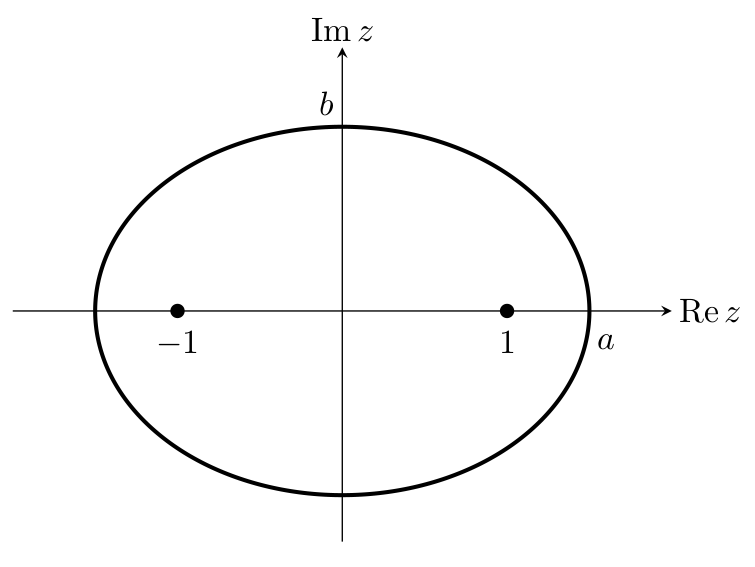
Комплексная плоскость
Пусть $z=x+iy$, тогда уравнение равносильно
\begin{equation*}
\sqrt{(x-1)^2 + y^2} + \sqrt{(x+1)^2+y^2} = 3.
\end{equation*}
Перенесём второе слагаемое вправо и возведём обе части равенства в квадрат:
\begin{equation*}
(x-1)^2 + y^2 = 9 - 6\sqrt{(x+1)^2+y^2} + (x+1)^2 + y^2,
\end{equation*}
или, сокращая,
\begin{equation}\label{eq:ell2}
6\sqrt{(x+1)^2+y^2} = 9 + 4x.
\end{equation}
Возведём обе части равенства \eqref{eq:ell2} в квадрат:
\begin{equation*}
36(x^2+2x+1+y^2) = 81 + 2\cdot36x+16x^2,
\end{equation*}
и далее
\begin{equation}\label{eq:ell3}
20x^2 + 36y^2 = 45.
\end{equation}
Перепишем уравнение \eqref{eq:ell3} в виде
\begin{equation*}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad \text{ где } a^2 = \frac{9}{4},\ b^2 = \frac{5}{4}.
\end{equation*}
Таким образом, исходное уравнение равносильно
каноническому уравнению эллипса.