Заметим, что все числа $z$, удовлетворяющие соотношению $|z| = 12$, образуют окружность с центром в нуле и радиусом $12$.
Соотношение $|w-3-4i|=5$ задаёт окружность с центром в точке $3 + 4i$ и радиусом $5$. В свою очередь, величина $|z-w|$ есть расстояние между точками $z$ и $w$. Таким образом, задача состоит в том, чтобы найти минимальное и максимальное расстояние между точками $z$ и $w$, лежащими на соответствующих окружностях. Построим эти окружности.

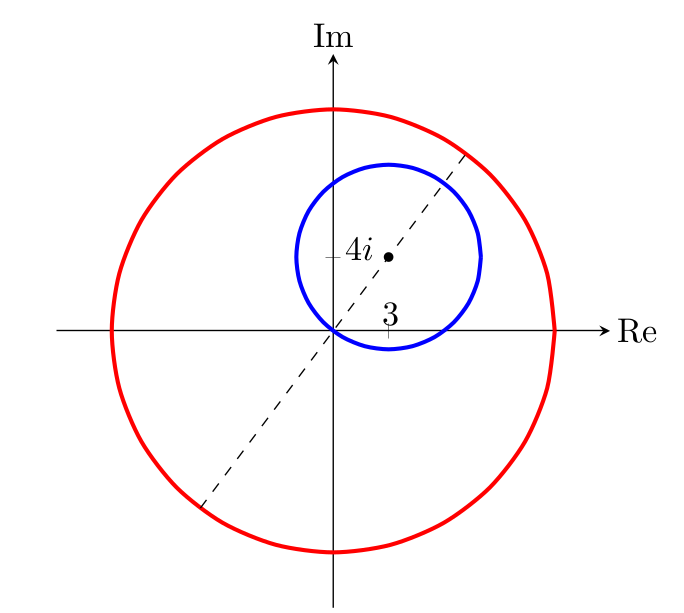
Из рисунка очевидно, что $12$ - максимальное расстояние, а $2$ - минимальное.