Преобразование Фурье [док.]
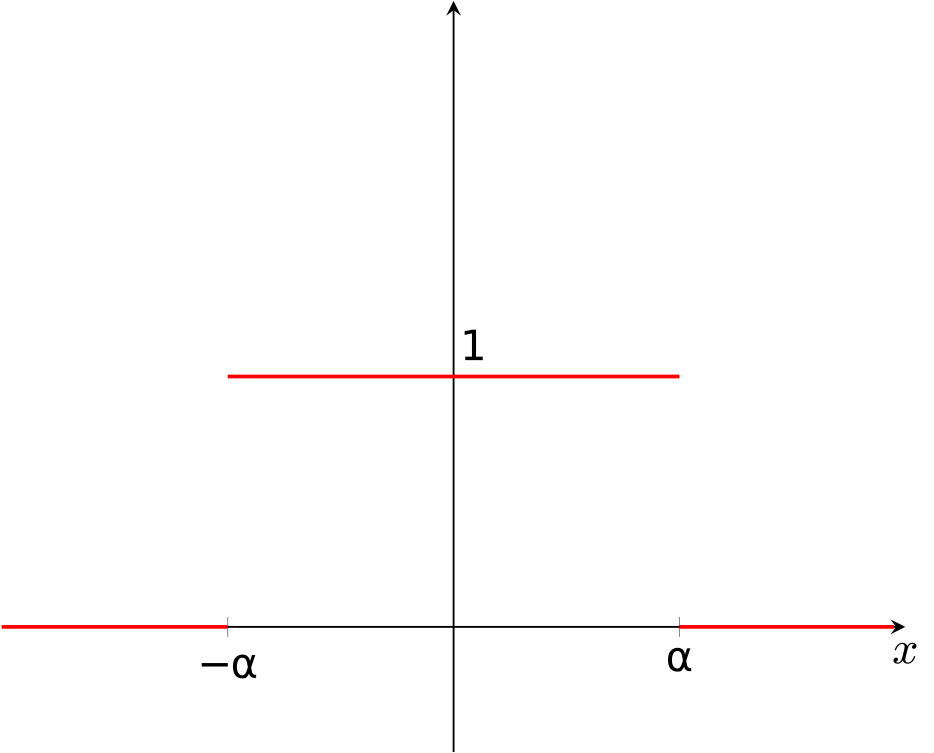
Вычислить преобразования Фурье прямоугольного импульса $$ f(x)= \begin{cases} 1, \text{ если } |x|<\alpha,\\ 0, \text{ если } |x|>\alpha. \end{cases} $$
Показать решение
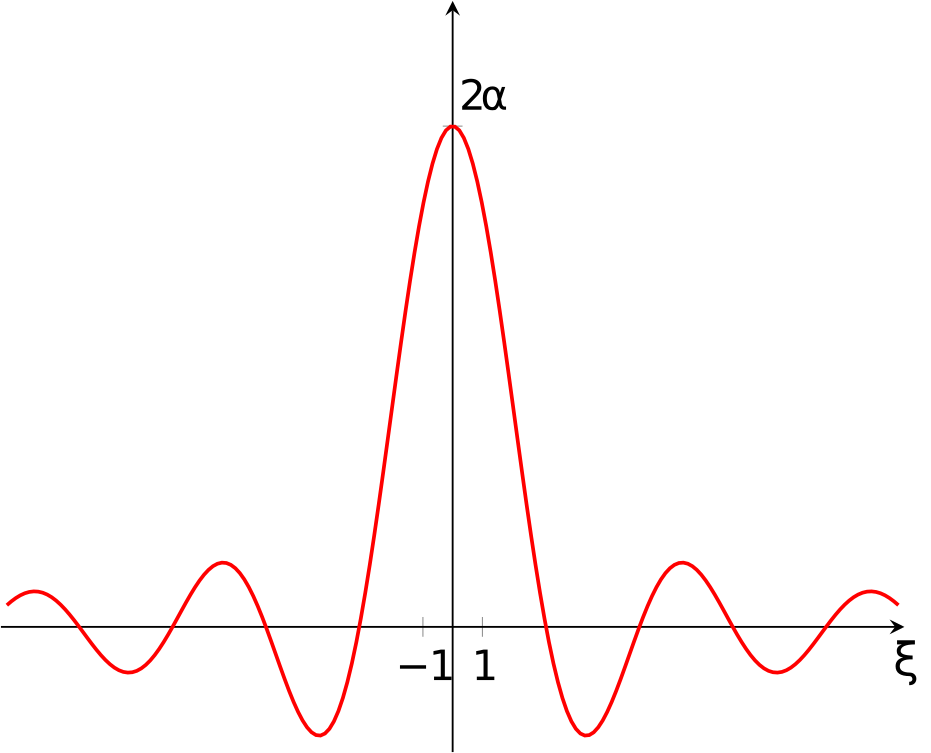
Имеем $$ \int\limits_{-\infty}^{+\infty}f(x)e^{-i x\xi}\, dx = \int\limits_{-\alpha}^{\alpha}1\cdot e^{-i x\xi}\, dx = \frac{e^{i \alpha\xi} - e^{-i \alpha\xi}}{i\xi}, $$ то есть $\hat f(\xi) = \frac{2\sin \alpha \xi}{ \xi}$.