Задача №590 |
| Тонкий стержень длины $4a$ лежит на оси $z$ так, что его центр
совпадает с началом координат. Стержень заряжен с линейной плотностью заряда
$\varkappa(z)=\left\{\begin{array}{l}
\varkappa_0, \, |z|\geqslant a\\
-\varkappa_0, \, |z|<a
\end{array}\right.$. Найти первый неисчезающий член разложения создаваемого им потенциала электрического поля $\varphi(r,\theta)$ на больших расстояниях $r\gg a$. |
|
|
|
Показать решение
|
|
Задача №589 |
| Тонкий стержень длины $4a$ лежит на оси $z$ так, что его центр
совпадает с началом координат. Стержень заряжен с линейной плотностью заряда
$\varkappa(z)=\varkappa_0 \left(\frac{|z|}{a}-1\right)$. Найти первый неисчезающий член разложения создаваемого им потенциала электрического поля $\varphi(r,\theta)$ на больших расстояниях $r\gg a$. |
|
|
|
Показать решение
|
|
Задача №588 |
| Тонкое непроводящее кольцо радиуса $a$ расположено в плоскости $xy$ так, что
его центр совпадает с началом координат. Кольцо заряжено с линейной плотностью заряда
$\varkappa (\alpha)=\varkappa_0\sin \alpha$, где $\alpha$ – угол от оси $x$. Найти первый неисчезающий член разложения создаваемого кольцом потенциала электрического поля
$\varphi(\vec{r})$ на больших расстояниях $r\gg a$. |
|
|
|
Показать решение
|
|
Задача №587 |
| Тонкое непроводящее кольцо радиуса $a$ расположено в плоскости $xy$ так, что
его центр совпадает с началом координат. Кольцо заряжено с линейной плотностью заряда
$\varkappa (\alpha)=\varkappa_0\cos \alpha$, где $\alpha$ – угол от оси $x$. Найти первый неисчезающий член разложения создаваемого кольцом потенциала электрического поля
$\varphi(\vec{r})$ на больших расстояниях $r\gg a$. |
|
|
|
Показать решение
|
|
Задача №559 |
| Найти изменение ёмкости плоского конденсатора $\delta C$ при внесении в него
маленького диэлектрического шарика с проницаемостью $\varepsilon$. Радиус шарика $a$
мал по сравнению с расстоянием от его центра до пластин конденсатора, расстояние между которыми $d$.
Краевыми эффектами пренебречь, до внесения шарика конденсатор был пуст. |

|
|
|
Показать решение
|
|
Задача №558 |
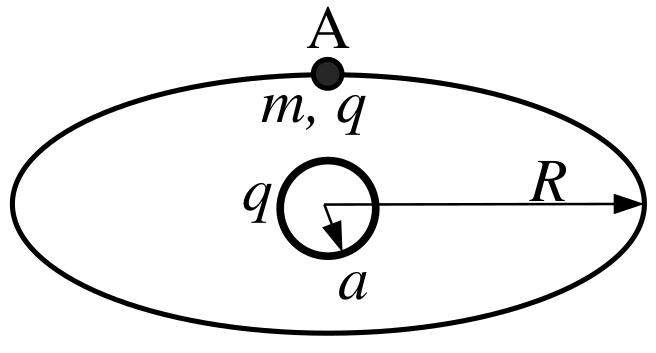
| Маленькая бусинка массой $m$, заряженная зарядом $q$, может двигаться без
трения вдоль горизонтально расположенной спицы, имеющей форму окружности радиуса $R$.
В центре этой окружности расположено равномерно заряженное зарядом $q$ тонкое кольцо, радиус которого $a\ll R$,
а его плоскость перпендикулярна плоскости спицы (таким образом, кольцо расположено вертикально). Центры кольца и спицы совпадают. Бусинка покоится в точке спицы A (см. рис., вектор, проведённый из центра кольца в точку A, перпендикулярен плоскости кольца). Какую
минимальную скорость необходимо сообщить бусинке для того, чтобы она вернулась в точку A, совершив полный оборот вокруг кольца вдоль спицы? |
|
|
|
Показать решение
|
|
Задача №551 |
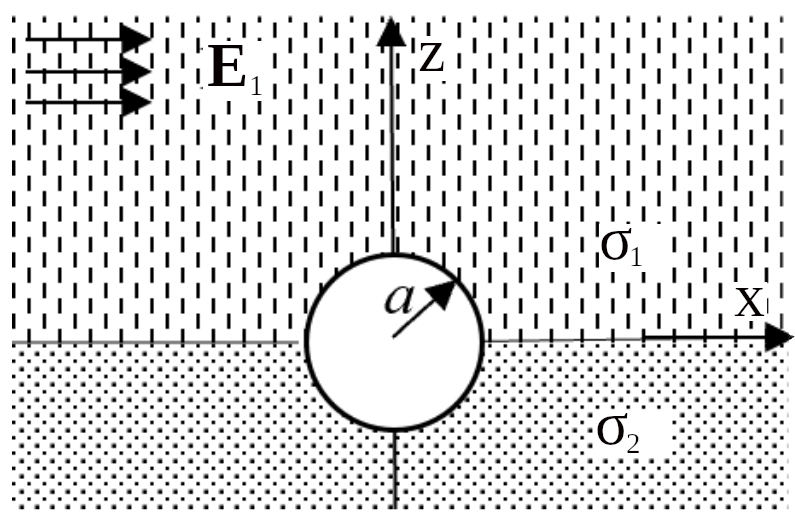
| Непроводящий шар радиуса $a$ помещен на плоскую границу раздела двух проводников с проводимостями $\sigma_1$ (верхнее полупространство) и $\sigma_2$ (нижнее полупространство) так, что центр шара совпадает с границей раздела проводников $z = 0$ и находится в точке начала координат
$(x, y) = (0, 0)$. В системе течёт ток так, что что линии тока
вдали от шара и границы раздела направлены параллельно к границе раздела, а напряженность поля вдали от шара однородна и равна $\vec{E}_1$ в проводнике с проводимостью $\sigma_1$. Определить напряженность электрического поля и плотность тока во всем пространстве. |
|
|
|
Показать решение
|
|
Задача №543 |
| Два постоянных точечных диполя расположены в одной
плоскости, как показано на рисунке. Во сколько раз
изменится потенциальная энергия взаимодействия диполей,
если один из диполей повернуть (см. рис.)? Угол $\alpha$,
указанный на рисунке, равен 60$^{\circ}$. |

|
|
|
Показать решение
|
|
Задача №542 |
| Два постоянных точечных диполя расположены в одной
плоскости, как показано на рисунке. Во сколько раз
изменится потенциальная энергия взаимодействия диполей,
если один из диполей повернуть (см. рис.)? Угол $\alpha$,
указанный на рисунке, равен 45$^{\circ}$. |

|
|
|
Показать решение
|
|
Задача №539 |
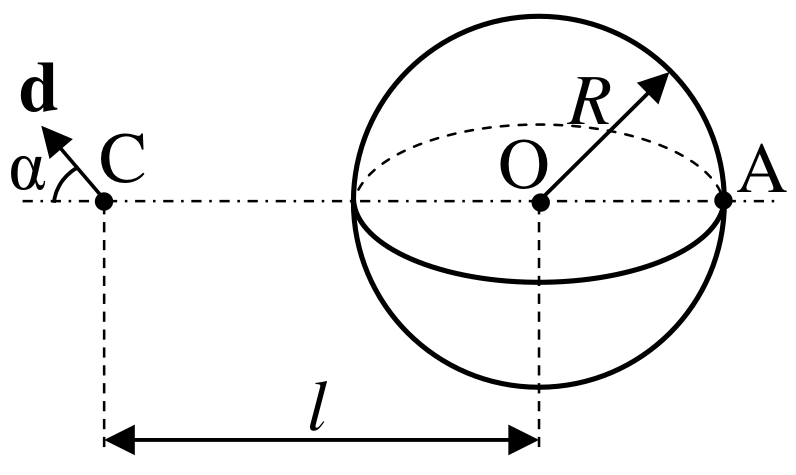
| На расстоянии $l$ от центра проводящей незаряженной
сферы радиуса $R<l$ расположен точечный диполь с
дипольным моментом $\vec{d}$, ориентированным под углом
$\alpha$ к прямой OC (см. рис.). Найти потенциал в точке A,
если потенциал на бесконечности равен нулю. |
|
|
|
Показать решение
|
|
Задача №538 |
| На расстоянии $l$ от центра проводящей незаряженной
сферы радиуса $R<l$ расположен точечный диполь с
дипольным моментом $\vec{d}$, ориентированным под углом
$\alpha$ к прямой OC (см. рис.). Найти потенциал в точке A,
если потенциал на бесконечности равен нулю. |

|
|
|
Показать решение
|
|
Задача №537 |
| В центре проводящей изолированной сферы радиуса $R$, несущей на себе полный заряд $Q$, находится точечный диполь с электрическим дипольным моментом $\vec{d}$. Найти поле во всем пространстве и плотность заряда на внешней и внутренней границах сферы. |

|
|
|
Показать решение
|
|
Задача №502 |
| Металлический шар радиуса $a$ помещен на плоскую границу раздела двух диэлектриков с диэлектрическими проницаемостями $\varepsilon_1$ (верхнее полупространство) и $\varepsilon_1$ (нижнее полупространство) так, что центр шара совпадает с границей раздела диэлектриков $z=0$ и находится в точке начала координат $(x=0, \,\,y=0)$. Система помещена во внешнее поле, направленное нормально к границе раздела, так, что электрическое поле вдали от шара и границы раздела однородно, а его напряженность в диэлектрике $\varepsilon_1$ равна $E_1$. Определить напряженность электрического поля и его индукцию во всем пространстве. |

|
|
|
Показать решение
|
|
Задача №490 |
| Точечный диполь $\vec{d}$ закреплён на расстоянии $h$ от плоской границы проводника. Найти распределение поверхностной плотности $\sigma$ индуцированного заряда на границе, если $\vec{d}$ параллелен границе. |

|
|
|
Показать решение
|
|
Задача №483 |
| Тонкая нить ($x$=0, $y$=0, $-a\leqslant z \leqslant a$) заряжена с линейной
плотностью заряда $\varkappa(z)=\varkappa_0 \sin \pi z/a$. Найти потенциал $\varphi(\vec{r})$ на расстояниях $r\gg a$. |

|
|
|
Показать решение
|
|
Задача №482 |
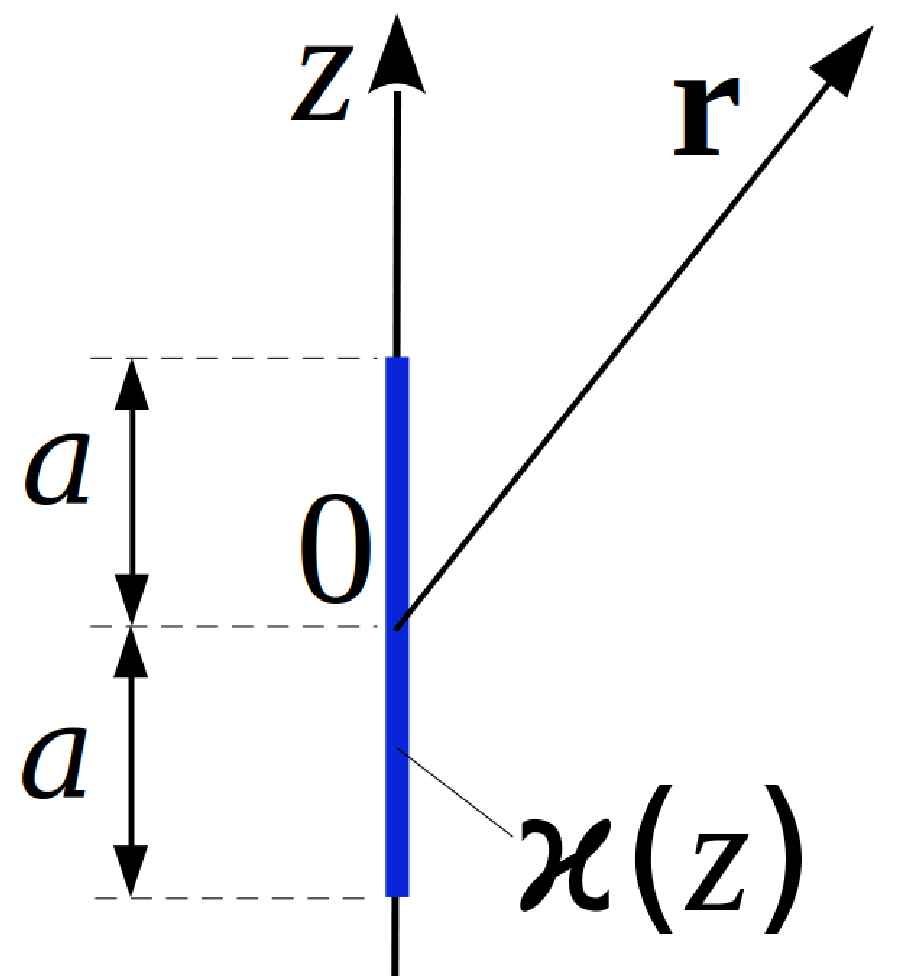
| Тонкая нить ($x$=0, $y$=0, $-a\leqslant z \leqslant a$) заряжена линейной
плотностью заряда $\varkappa(z)=\varkappa_0 z^3/a^3$. Найти потенциал $\varphi(\vec{r})$ на расстояниях $r\gg a$. |
|
|
|
Показать решение
|
|
Задача №464 |
| По бесконечной тонкой проводящей пластинке с
круговым вырезом бежит ток, поверхностная плотность которого вдали от выреза
$\vec{J}_0 =J_0\vec{e}_x$.
Найти распределение тока на всей пластине $\vec{J}(\vec{r},\alpha)$. |

|
|
|
Показать решение
|
|
Задача №463 |
| Круговой вырез в бесконечной тонкой проводящей пластине заполнен идеально проводящим тонким диском. По пластине бежит ток, поверхностная
плотность, которого вдали от выреза $\vec{J}_0 =J_0\vec{e}_x$. Найти
распределение тока на всей пластине $\vec{J}(r,\alpha)$. |

|
|
|
Показать решение
|
|
Задача №458 |
| Шар радиуса $a$ заряжен с объёмной плотностью $\rho(\theta) = \rho_0 \cos \theta$,
где $\theta$ – угол с осью $Oz$, проходящей через центр O шара.
Найти электрическое поле $\vec{E}(\vec{r})$ во всём пространстве. |
|
|
|
Показать решение
|
|
Задача №370 |
| Одно из оснований непроводящего цилиндра радиуса $R$ длины $L$ равномерно заряжено зарядом $q$, а к другому приклеена соосно непроводящая полусфера того же радиуса, равномерно заряженная зарядом $-q$. Найти дипольный момент получившейся системы зарядов. |

|
|
|
Показать решение
|
|
Задача №369 |
| Боковая поверхность непроводящего цилиндра радиуса $R$ длины $L$ равномерно заряжена зарядом $q$.
К одному из оснований приклеена соосно непроводящая полусфера того же радиуса, равномерно заряженная зарядом $-q$. Найти дипольный момент получившейся системы зарядов. |

|
|
|
Показать решение
|
|
Задача №331 |
| Тонкое круговое кольцо радиуса $a$ расположено в плоскости $xy$ и заряжено с линейной плотностью $\varkappa(\alpha)=\varkappa_0+\varkappa_1\cos\alpha$ (см. рис.). Найти
первые два неисчезающих члена разложения потенциала $\varphi(\vec{r})$ вблизи начала координат $(r\ll a)$. Константу в выражении потенциала выбрать из условия
$\varphi(\infty)=0$. |

|
|
|
Показать решение
|
|
Задача №321 |
| Точечный электрический диполь находится между двумя точечными зарядами $q_1$ и $q_2$ на расстоянии $r$ от каждого. Дипольный момент $\vec{d}$ ориентирован вдоль прямой, соединяющей точечные заряды. Найти силу, действующую на диполь. |

|
|
|
Показать решение
|
|
Задача №320 |
| Найти изменение дипольного момента однородного диэлектрического шара с проницаемостью $\varepsilon$ и радиусом $R$, помещенного в однородное электрическое поле $\vec{E}$, при поднесении к нему такого же шара на расстояние $a$ $(a\gg R)$. Рассмотреть случай, когда электрическое поле параллельно линии, соединяющей центры шаров. |
|
|
|
Показать решение
|
|
Задача №319 |
| Четыре одинаковых заряда $q$ размещены в углах квадрата со стороной $l$. Найти изменение потенциала $\delta \varphi(\vec{r})$ на больших расстояниях, если в центр
квадрата на одинаковом удалении от каждого из зарядов поместить незаряженную металлическую сферу радиуса $a$ $(r\gg l>a\sqrt{2})$. |

|
|
|
Показать решение
|
|
Задача №318 |
| В углах квадрата со стороной $l$ находятся четыре заряда $q$, $-q$, $q$, и $-q$. В центр квадрата на одинаковом удалении от каждого из зарядов помещена незаряженная металлическая сфера радиуса $a$. Найти потенциал $\varphi(\vec{r})$ на больших расстояниях от этой системы ($r\gg l>a\sqrt{2}$). |

|
|
|
Показать решение
|
|
Задача №315 |
| Два заряда $q_1$ и $q_2$ расположены в точках с декартовыми
координатами $(x_1,0,0)$ и $(0,y_2,0)$ соответственно. Найти величину заряда $q$ и декартовые координаты точки, в которую
его нужно поместить, чтобы величина электрического поля на больших расстояниях от системы зарядов была как можно меньше. |
|
|
|
Показать решение
|
|
Задача №314 |
| Два заряда $q_1$ и $q_2$ расположены в точках с декартовыми
координатами $(0,y_1,0)$ и $(x_2,0,0)$ соответственно. Найти величину заряда $q$ и декартовые координаты точки, в которую
его нужно поместить, чтобы величина электрического поля на больших расстояниях от системы зарядов была как можно меньше. |
|
|
|
Показать решение
|
|
Задача №268 |
| В пространство с однородным электрическим полем $E_0$
поместили диэлектрический цилиндр длиной $l$ и сечением $S$ $(l\ll S )$
с диэлектрической проницаемостью $\varepsilon$.
Ось цилиндра и направление электрического поля $E_0$ совпадают. Оценить электрическое поле,
создаваемое цилиндром на расстояниях $r\gg l$. |
|
|
|
Показать решение
|
|
Задача №263 |
| Два равномерно заряженных прямых отрезка с зарядами $q$, $-q$ и с длинами $2a$, $2b$ расположены в плоскости $(x,y)$,
как показано на рисунке. Найти дипольный момент $d$ и первый ненулевой член в разложении потенциала
$\varphi(x,y,z)$, вдали от системы зарядов $\sqrt{x^2+y^2+z^2}\gg a,b$. |

|
|
|
Показать решение
|
|
Задача №262 |
| Два равномерно заряженных прямых отрезка с зарядами $q$, $-q$ и с длинами $2a$, $2b$ расположены в плоскости $(x,y)$,
как показано на рисунке. Найти дипольный момент $d$ и первый ненулевой член в разложении потенциала
$\varphi(x,y,z)$, вдали от системы зарядов $\sqrt{x^2+y^2+z^2}\gg a,b$. |

|
|
|
Показать решение
|
|
Задача №259 |
| Найти в лабораторной системе отсчета скалярный и векторный потенциалы релятивистской нейтральной частицы
с дипольным электрическим моментом $\vec{d}_0$ (в собственной системе отсчета), которая движется перпендикулярно $\vec{d}_0$ со скоростью $v\sim c$. |
|
|
|
Показать решение
|
|
Задача №246 |
| Найти в лабораторной системе отсчета скалярный и векторный потенциалы релятивистской нейтральной частицы
с магнитным моментом $\vec{m}_0$ (в собственной системе отсчета), которая движется вдоль направления $\vec{m}_0$ со скоростью $v\sim c$. |
|
|
|
Показать решение
|
|
Задача №217 |
| Оценить диэлектрическую проницаемость кристалла, имеющего структуру простой кубической решетки, в узлах которой находятся металлические шарики диаметром $d\ll a$, где $a$ – постоянная решетки. |
|
|
|
Показать решение
|
|
Задача №213 |
| На бесконечно протяженном проводнике, поверхность которого образует прямой двугранный угол,
имеется сферический выступ радиуса $a$ с центром на ребре. Заряд $q$ поместили в плоскости,
перпендикулярной граням двугранного угла, проходящей через центр сферического
выступа, на расстоянии $a$ от каждой из граней. Найти первый неисчезающий член в разложении потенциала
$\varphi(\vec{r})$ на больших расстояниях $r\gg a$. |
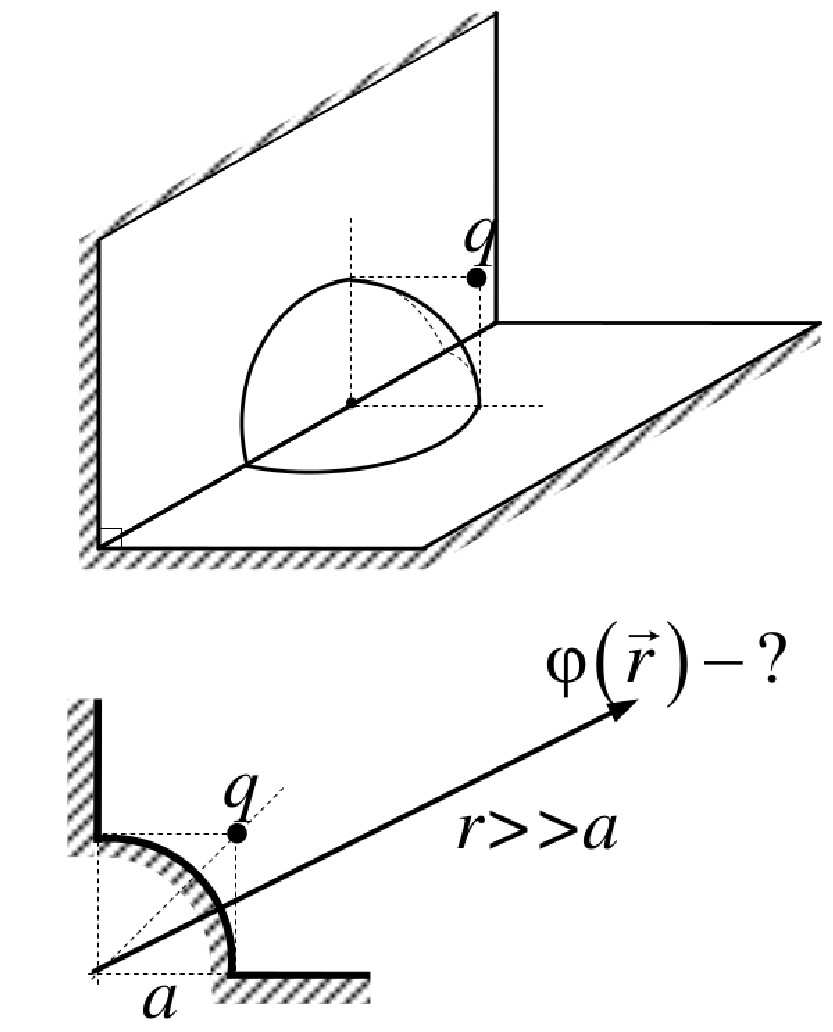
|
|
|
Показать решение
|
|
Задача №212 |
| Два одинаковых точечных заряда $q$ закреплены на расстоянии $2l$
друг от друга. Между ними помещают незаряженный проводящий
шарик радиуса $a < l$, так что центр шарика оказывается посередине
между зарядами (см. рисунок). Найти первый неисчезающий член в
разложении изменения потенциала $\Delta\varphi(\vec{r})$ на больших расстояниях
$r\gg 2l$, возникшего за счет шарика. |

|
|
|
Показать решение
|
|
Задача №150 |
| Незаряженный диэлектрический шар радиуса $b$, содержащий
внутри себя проводящий шар радиуса $a<b$, находится в однородном
внешнем электрическом поле $\vec{E}_0$. Найти распределение потенциала во
внешнем пространстве $r>b$, в диэлектрическом слое $a<r<b$ и в металлическом шаре. |

|
|
|
Показать решение
|
|
Задача №149 |
| Два кольца одинакового радиуса $R$ расположены во взаимно перпендикулярных плоскостях так,
что обод одного кольца проходит через центр другого (см. рисунок). Кольца заряжены однородно по длине равными по
величине, но противоположными по знаку зарядами $+Q$ и $–Q$. Найти
первый неисчезающий член потенциала $\varphi(r,\theta)$ на больших расстояниях
$r\gg R$. Угол $\theta$ отсчитывать от линии, соединяющей центры колец. |

|
|
|
Показать решение
|
|
Задача №145 |
| Равномерно заряженные прямые стержни с зарядами $q$ и $-q$ расположены в плоскости $(x,y)$, как показано на рисунке.
Длины стержней равны $a$ и $b$ (смотри рисунок). Найти первый неисчезающий член потенциала $\varphi(x,y,z)$
на больших расстояниях $\sqrt{x^2+y^2+z^2}\gg a,b$. |

|
|
|
Показать решение
|
|
Задача №133 |
| Найти энергию взаимодействия и силу, действующую на малое заряженное по объему тело с
квадрупольным моментом $Q_{ij}$ (полный заряд тела и его дипольный момент равны нулю) со стороны
внешнего слабонеоднородного электрического поля $\vec{E}(\vec{r})$. |
|
|
|
Показать решение
|
|
Задача №130 |
| В плоскости $z=0$, разделяющей два полупространства, заполненных диэлектриками
с $\varepsilon_1\; (z<0)$ и $\varepsilon_2\; (z>0)$, расположены точечные заряды
в вершинах равнобедренного прямоугольного треугольника, как показано на
рисунке. Найти дипольный член в разложении потенциала $\varphi_{1,2}(x,y,z)$ для
обеих областей на расстояниях, много больших, чем $a$. |

|
|
|
Показать решение
|
|
Задача №129 |
| В плоскости $z=0$, разделяющей два полупространства, заполненных диэлектриками
с $\varepsilon_1\; (z<0)$ и $\varepsilon_2\; (z>0)$, расположены точечные заряды
в вершинах равнобедренного прямоугольного треугольника, как показано на
рисунке. Найти дипольный член в разложении потенциала $\varphi_{1,2}(x,y,z)$ для
обеих областей на расстояниях, много больших, чем $a$. |

|
|
|
Показать решение
|
|
Задача №19 |
| В бесконечной среде с проводимостью $\sigma$ шёл однородный ток с плотностью $j_0$ вдоль оси $x$.
В среде возникла цилиндрическая полость радиуса $a$
бесконечной длины (внутри полости $\sigma_{in}=0$). Ось цилиндра перпендикулярна
направлению тока $j_0$. Найти результирующее распределение токов $j(r,\alpha)$. |

|
|
|
Показать решение
|
|
Задача №18 |
| Заряды $+q$, $-\frac{2}{3}q$ и $-\frac{1}{3}q$ расположены в вершинах равностороннего треугольника со стороной $a$,
как показано на рисунке. Найти первый неисчезающий член разложения потенциала $\varphi(x,y,z)$ на расстояниях
$\sqrt{x^2+y^2+z^2}\gg a$ |

|
|
|
Показать решение
|
|
Задача №17 |
| Два равномерно заряженных отрезка длиной $a$ с зарядами $q$ и точечный заряд $-2q$ расположены в плоскости $(x,y)$, как показано на рисунке. Найти первый
ненулевой член мультипольного разложения потенциала как функцию $\varphi(x$,$y$,$z)$ на большом расстоянии
($r\gg a$) от начала координат. |

|
|
|
Показать решение
|
|
Задача №16 |
| Пространство между двумя плоскими электродами заполнено проводящей средой
с проводимостью $\sigma $. Нижний электрод очень толстый, его удельное
сопротивление близко к нулю. На этом электроде имеется
небольшой полуцилиндрический выступ радиуса $a$.
Из верхнего электрода в нижний идет ток,
плотность которого у верхнего электрода практически постоянна и равна
$\vec{j}_{0}$. Найти величину тока $J$, идущего через выступ на единицу его
длины |

|
|
|
Показать решение
|
|
Задача №15 |
| Сплошной бесконечно длинный цилиндр радиуса $a$ с проводимостью $\sigma
_{\mathrm{1}}$ находится в однородном проводнике с проводимостью $\sigma
_{\mathrm{2}}$. Внутри цилиндра действует стороннее однородное поле
$\vec{E}_{ext}$, направленное перпендикулярно оси
цилиндра. Найти распределение тока во всем пространстве. |
|
|
|
Показать решение
|
|
Задача №14 |
| На расстоянии $a$ от полупространства, заполненного однородным
диэлектриком с проницаемостью $\varepsilon $, закреплен центр точечного
диполя с дипольным моментом $d$. Диполь может свободно вращаться, изменяя
направление вектора $\vec{d}$. Параллельно границе полупространства
приложено однородное внешнее электрическое поле $\vec{E}$. Найти
установившееся равновесное значение угла $\alpha $ между направлением
$\vec{E}$ и $\vec{d}$ |

|
|
|
Показать решение
|
|
Задача №13 |
| В плоской границе раздела двух полупространств с диэлектрическими проницаемостями $\varepsilon_1$ и $\varepsilon_2$
находится равномерно заряженное кольцо радиуса $a$ с общим зарядом $q$. Найти два первых ненулевых члена разложения
потенциала $\varphi (r,\theta )$ для расстояний $r\gg a$ |

|
|
|
Показать решение
|
|
Задача №10 |
Заземление представляет собой идеально проводящий шар радиуса $a$, помещенный в бесконечную
среду с проводимостью $\sigma$.
1. Найти сопротивление заземления.
2. Найти сопротивление заземления,
если в среде образовалась сферическая полость радиуса $b$, заполненная идеальным проводником
(внутри полости $\sigma_{in}=\infty$), расстояние между центрами заземляющего шара и полости равно $l$.
3. Найти сопротивление заземления, если полость не проводит ток (внутри полости $\sigma_{in}=0$). Качественно
нарисовать линии тока во всех случаях, $l>a+b$, $a\ll b,l-b$. |
|
|
|
Показать решение
|
|
Задача №8 |
| Два тонких кольца радиусами $a$ и $b$, расположенные соосно в плоскостях $z=0$ и $z=h$, равномерно заряжены зарядами
$q$ и $-q$. Найти два первых ненулевых члена разложения потенциала на больших расстояниях $r$ |
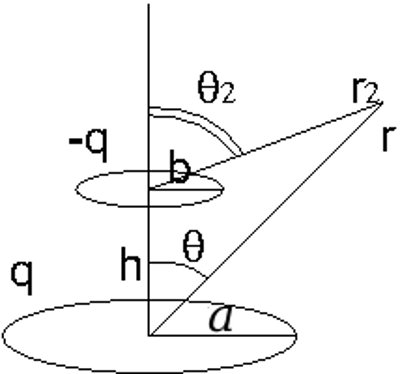
|
|
|
Показать решение
|
|
Задача №7 |
| Две бесконечные параллельные нити, расположенные
на расстоянии $a$ друг от друга, равномерно заряжены с линейными плотностями
$+\varkappa $ и $-\varkappa $. Найти силу, действующую на заряд $q$, удаленный на
расстояние $R\gg a$ от нитей. Угол между векторами
$\vec{R}$ и $\vec{a}$ равен $\alpha $ |

|
|
|
Показать решение
|
|