Задача №571 |
| Поверхность стекла ($n_{\text{ст}}$=1.5) смочена тонким слоем спирта ($n_{\text{сп}}$=1.36).
В эксперименте измеряется спектр отражения и пропускания слоя спирта
при освещении рассеянным солнечным светом. Регистрируется свет, отражённый и прошедший перпендикулярно поверхности. Оказалось, что в спектре отражения наблюдается единственный максимум в видимом диапазоне (от 380 нм до 780 нм), который приходится на длину волны $\lambda_0$=385 нм (фиолетовый цвет). Определить на какую длину волны приходится максимум спектра пропускания в видимом диапазоне. Толщина стекла много больше длины когерентности света. |

|
|
|
Показать решение
|
|
Задача №570 |
| Тонкий слой бензина ($n_{\text{б}}$ = 1.4) покрывает поверхность воды ($n_{\text{в}}$ = 1.3),
налитой в прозрачную кювету. В эксперименте измеряется спектр отражения и пропускания слоя при освещении рассеянным солнечным светом. Регистрируется свет, отражённый и прошедший перпендикулярно поверхности. Оказалось, что в спектре отражения наблюдается единственный максимум в видимом диапазоне (от 380 нм до 780 нм), который
приходится на длину волны $\lambda_0$ = 780 нм (красный цвет). Определить на
какую длину волны приходится максимум спектра пропускания в видимом диапазоне. Толщина слоя воды и стенок кюветы много больше длины когерентности света. |

|
|
|
Показать решение
|
|
Задача №536 |
| На интерферометр Фабри-Перо, состоящий из одинаковых плоских зеркал, нормально падает плоская монохроматическая волна. Энергетические коэффициенты отражения и прохождения $R$ и $T$, причём $1-R-T=T$. Найти зависимость энергетического коэффициента пропускания интерферометра от длины волны и максимальное (резонансное) значение этого коэффициента пропускания. |
|
|
|
Показать решение
|
|
Задача №527 |
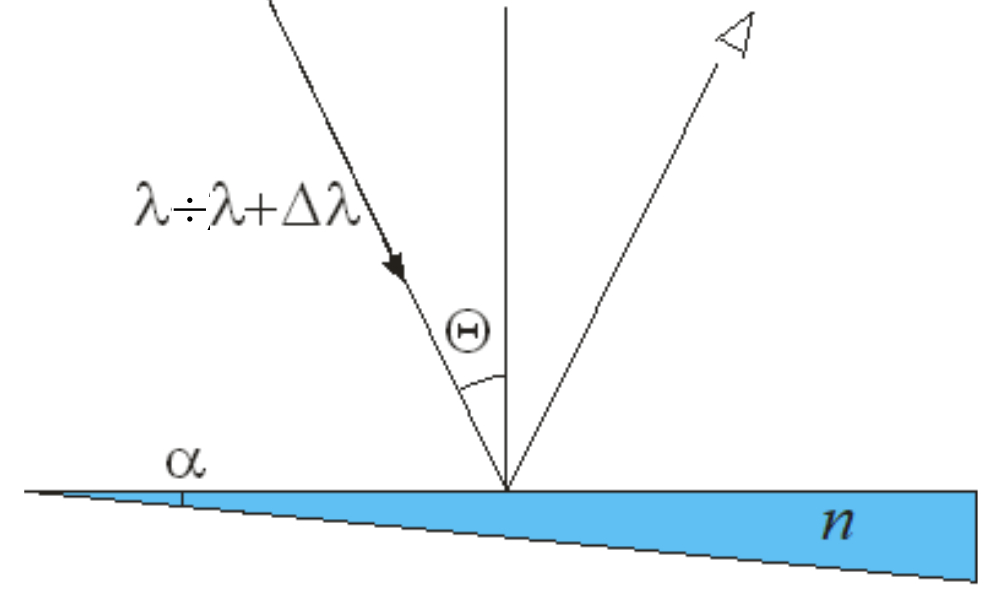
| На прозрачный клин c углом при вершине $\alpha\ll 1$, изготовленный из материала с показателем преломления $n$, под углом $\theta$ к нормали падает плоская квазимонохроматическая волна со спектром длин волн в диапазоне $\lambda \div \lambda+\Delta \lambda$. Оценить размер интерференционной картины, наблюдаемой глазом на поверхности клина. |
|
|
|
Показать решение
|
|
Задача №526 |
| На прозрачный клин c толщиной $h(x) =\alpha x^2$, изготовленный из материала с показателем преломления $n$, под углом $\theta$ к нормали падает плоская квазимонохроматическая волна со спектром длин волн в диапазоне $\lambda \div \lambda+\Delta \lambda$. Оценить размер интерференционной картины, наблюдаемой глазом на поверхности клина. |

|
|
|
Показать решение
|
|
Задача №439 |
| Найти радиусы интерференционных колец Ньютона в отраженном
свете с длиной волны $\lambda$ на воздушном клине между плоско-выпуклой
и плоско-вогнутой линзами (см. рисунок) с радиусами кривизны $R_1$ и $R_2$. |

|
|
|
Показать решение
|
|
Задача №438 |
| Найти радиусы интерференционных колец Ньютона в отраженном
свете с длиной волны $\lambda$ на воздушном клине между двумя плоско-выпуклыми линзами (см. рисунок)
с радиусами кривизны $R_1$ и $R_2$. |

|
|
|
Показать решение
|
|
Задача №437 |
| Интерферометр состоит из идеально отражающей поверхности (зеркала) и
расположенной перед ним на расстоянии $l$ проводящей плоскости, поверхностный
ток в которой удовлетворяет закону Ома, то есть $J=\sigma^* E$. При каких
значениях $\sigma^*$ и $l$ интерферометр не отражает (коэффициент отражения
$R=0$) падающую по нормали плоскую монохроматическую волну с волновым
вектором $\vec{k}$? |

|
|
|
Показать решение
|
|
Задача №351 |
| Тонкий прозрачный слой толщиной $d$ с показателем преломления $n_2$ разделяет
прозрачные среды с показателем преломления $n_1$ и $n_3$ $(n_1 > n_2 > n_3 > 1)$. На этот слой из области
c $n_1$ падает нормально к его поверхности ЭМ волна. При этом коэффициент отражения
точно равен 0. Найти $n_2$ и $n_3$, если известно, что $n_1 = 6/5$,
$d=800$ нм, $\lambda = 400$ нм, где $\lambda$ – длина волны той же частоты в вакууме. |
|
|
|
Показать решение
|
|
Задача №350 |
| Тонкий прозрачный слой толщиной $d$ с показателем преломления $n_2$ разделяет
прозрачные среды с показателем преломления $n_1$ и $n_3$ $(n_1 > n_2 > n_3 > 1)$. На этот слой из области
c $n_1$ падает нормально к его поверхности ЭМ волна. При этом коэффициент отражения
точно равен 0. Найти $n_2$ и $n_3$, если известно, что $n_1 = 4/3$,
$d=600$ нм, $\lambda = 400$ нм, где $\lambda$ – длина волны той же частоты в вакууме. |
|
|
|
Показать решение
|
|
Задача №300 |
| Тонкая (не толще 200 нм) мыльная пленка с показателем преломления $n = 1.33$,
натянутая на вертикальную раму, за счет силы тяжести внизу несколько толще, чем вверху.
При наблюдении перпендикулярно поверхности в белом отраженном свете пленка имеет зеленоватый оттенок,
максимально отражая свет с длиной волны $\lambda_1$ вверху и $\lambda_2$ внизу. На сколько толщина пленки внизу больше, чем
вверху, если $\lambda_2-\lambda_1 = 50$ нм? |
|
|
|
Показать решение
|
|
Задача №299 |
| Гладкая поверхность кремниевой пластины покрыта тонким однородным слоем окисла с показателем
преломления $n = 1.46$. При наблюдении перпендикулярно поверхности в отраженном белом
свете она имеет красноватый оттенок, максимально отражая свет с длиной волны $\lambda_1$. Пластину поместили на некоторое время в печь. Теперь она максимально отражает свет с длиной волны $\lambda_2$. Насколько увеличилась при этом толщина слоя окисла, если $\lambda_2-\lambda_1=90\,\, нм$? Конечная толщина окисла не превышает 300 нм. Показатель преломления кремния больше $n$. |
|
|
|
Показать решение
|
|
Задача №241 |
| На поверхности воды тонким слоем разлит бензин. Если посмотреть на однородный по толщине участок пленки бензина сверху,
то он кажется красным ($\lambda_0$=760 нм). Определите, на какой минимальный угол $\alpha$ нужно изменить угол зрения,
чтобы пленка стала казаться фиолетовой ($\lambda$=380 нм).
Показатели преломления бензина и воды равны $n_б$=1.4 и $n_в$=1.3 соответственно. |

|
|
|
Показать решение
|
|
Задача №240 |
| Две тонкие диэлектрические прозрачные пленки одинаковой субмикронной толщины с одинаковым показателем преломления
нанесены на разные подложки.
У первой подложки показатель преломления меньше, чем у пленки, а у второй – больше.
Определите, какой цвет $\lambda$ имеет пленка, лежащая на первой подложке, если пленка, лежащая на второй подложке,
имеет красный цвет ($\lambda_0$=700 нм), соответствующий первому порядку интерференционного максимума.
На пленки смотрят под прямым углом к поверхности. |

|
|
|
Показать решение
|
|
Задача №197 |
| На тонком стеклянном клине с показателем преломления $n = 1.5$
длиной $l = 10$ см при наблюдении под прямым углом в свете с длиной
волны $\lambda$=0.5 мкм умещается 6 интерференционных полос равной
толщины. Оценить угол $\alpha$ клина. |

|
|
|
Показать решение
|
|
Задача №196 |
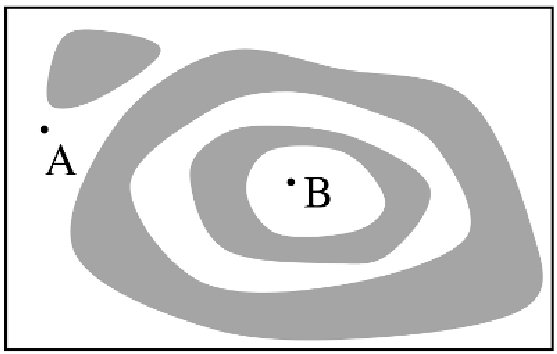
| На рисунке схематически изображена картина интерференционных
полос равной толщины на тонкой пленке с показателем преломления
$n = 2$, наблюдаемая по нормали к ней в свете с длиной волны
$\lambda = 0.5\; мкм$. Оцените перепад толщины $\Delta h$ между точками $A$ и $B$,
считая, что на отрезке $AB$ толщина пленки меняется монотонно. |
|
|
|
Показать решение
|
|
Задача №69 |
| Пучки света, отраженные двумя поверхностями стеклянной пластинки толщиной $h$ с
показателем преломления $n$, создают интерференционные полосы на экране (см.
рисунок). Источником света служит точечный квазимонохроматический источник с
шириной спектра $\Delta \omega \ll \omega_0$
вблизи основной частоты $\omega_0$. Аппроксимируя истинный контур
спектральной линии прямоугольником шириной $\Delta \omega $, найти значение
угла $\theta =\theta_0$, характеризующего положение точки на
экране, где видность полос обращается в нуль, если $h=\pi c/\Delta\omega$,
$H/h \gg 1,\; 1<n<\sqrt 2$. |

|
|
|
Показать решение
|
|
Задача №49 |
| Собирающая линза положена на плоскую стеклянную пластину, причем вследствие
попадания пыли между линзой и пластиной есть зазор. Диаметры 5 и 15-го
темных колец Ньютона, наблюдаемых в отраженном свете ($\lambda=589 нм$),
равны соответственно 0,7 и 1,7 мм. Определить радиус
кривизны поверхности линзы, обращенной к пластинке. Влиянием пылинок на
прохождение света пренебречь. |

|
|
|
Показать решение
|
|